کامپیوتر و ریاضی با علی رضا نقش

3-یادگیری ماشین کوانتومی

کاربرد یادگیری کلاسیک در مسائل کوانتومی [ ویرایش ]

اطلاعات بیشتر: یادگیری ماشینی در فیزیک

اصطلاح "یادگیری ماشین کوانتومی" گاهی اوقات به یادگیری ماشین کلاسیک بر روی داده های سیستم های کوانتومی اشاره دارد. یک مثال اساسی از این توموگرافی حالت کوانتومی است ، که در آن یک حالت کوانتومی از اندازه گیری آموخته می شود. کاربردهای دیگر شامل یادگیری همیلتونی ها [96] و تولید خودکار آزمایش های کوانتومی است. [20]

نظریه یادگیری کوانتومی [ ویرایش ]

نظریه یادگیری کوانتومی یک تحلیل ریاضی از تعمیم‌های کوانتومی مدل‌های یادگیری کلاسیک و افزایش‌های احتمالی یا سایر پیشرفت‌هایی که ممکن است ارائه کنند را دنبال می‌کند. چارچوب بسیار شبیه به نظریه یادگیری محاسباتی کلاسیک است ، اما یادگیرنده در این مورد یک دستگاه پردازش اطلاعات کوانتومی است، در حالی که داده ها ممکن است کلاسیک یا کوانتومی باشند. تئوری یادگیری کوانتومی را باید با یادگیری ماشینی پیشرفته کوانتومی که در بالا مورد بحث قرار گرفت، مقایسه کرد، جایی که هدف در نظر گرفتن مسائل خاص و استفاده از پروتکل‌های کوانتومی برای بهبود پیچیدگی زمانی الگوریتم‌های کلاسیک برای این مسائل بود. اگرچه نظریه یادگیری کوانتومی هنوز در حال توسعه است، نتایج جزئی در این جهت به دست آمده است. [97]

نقطه شروع در تئوری یادگیری معمولاً یک کلاس مفهومی است، مجموعه ای از مفاهیم ممکن. معمولاً یک مفهوم تابعی در برخی دامنه ها است، مانند{0،1}� $\{0,1\}^{n}$ . برای مثال، کلاس مفهومی می‌تواند مجموعه فرمول‌های فرمول نرمال منفصل (DNF) روی n بیت یا مجموعه مدارهای بولی با عمق ثابت باشد. هدف یادگیرنده یادگیری (دقیقا یا تقریباً) یک مفهوم هدف ناشناخته از این کلاس مفهومی است. یادگیرنده ممکن است به طور فعال با مفهوم هدف تعامل داشته باشد یا به طور منفعلانه نمونه هایی از آن دریافت کند.

در یادگیری فعال، یک یادگیرنده می تواند پرس و جوهای عضویت را برای مفهوم هدف c بپرسد و مقدار c(x) آن را در ورودی های x انتخاب شده توسط یادگیرنده بپرسد. سپس یادگیرنده باید مفهوم هدف دقیق را با احتمال زیاد بازسازی کند. در مدل یادگیری دقیق کوانتومی، یادگیرنده می تواند پرس و جوهای عضویت را در برهم نهی کوانتومی ایجاد کند. اگر پیچیدگی یادگیرنده با تعداد جستارهای عضویتی که ایجاد می کند سنجیده شود، آنگاه یادگیرندگان دقیق کوانتومی می توانند به صورت چندجمله ای کارآمدتر از یادگیرندگان کلاسیک برای برخی از کلاس های مفهومی باشند، اما نه بیشتر. [98] اگر پیچیدگی با مقدار زمانی که یادگیرنده استفاده می‌کند اندازه‌گیری شود، کلاس‌های مفهومی وجود دارند که می‌توانند به طور مؤثر توسط یادگیرندگان کوانتومی یاد بگیرند، اما نه توسط یادگیرندگان کلاسیک (تحت فرضیات نظریه پیچیدگی قابل قبول). [98]

یک مدل طبیعی از یادگیری غیرفعال ، احتمالاً یادگیری تقریباً صحیح (PAC) Valiant است . در اینجا یادگیرنده نمونه های تصادفی (x,c(x)) را دریافت می کند، که در آن x بر اساس توزیع ناشناخته D توزیع می شود. هدف یادگیرنده خروجی دادن یک تابع فرضیه h است به طوری که h(x)=c(x) با احتمال زیاد هنگامی که x مطابق D رسم می شود. یادگیرنده باید بتواند برای هر D و هر مفهوم هدف c در کلاس مفهومی خود، h تقریباً درستی تولید کند. می‌توانیم مثال‌های تصادفی را با مثال‌های کوانتومی قوی‌تر جایگزین کنیم $\sum _{x}{\sqrt {D(x)}}|x,c(x)\rangle$ . در مدل PAC (و مدل آگنوستیک مربوطه)، این به طور قابل توجهی تعداد نمونه‌های مورد نیاز را کاهش نمی‌دهد: برای هر کلاس مفهومی، پیچیدگی نمونه کلاسیک و کوانتومی تا فاکتورهای ثابت یکسان است. [99] با این حال، برای یادگیری تحت توزیع ثابت D، مثال‌های کوانتومی می‌توانند بسیار مفید باشند، برای مثال برای یادگیری DNF تحت توزیع یکنواخت. [100] هنگام در نظر گرفتن پیچیدگی زمانی، کلاس‌های مفهومی وجود دارد که می‌توانند توسط یادگیرندگان کوانتومی، حتی از مثال‌های کلاسیک، به‌طور کارآمد PAC یاد بگیرند، اما نه توسط یادگیرندگان کلاسیک (دوباره، تحت مفروضات نظری پیچیدگی قابل قبول). [98]

این نوع یادگیری غیرفعال همچنین رایج‌ترین طرح در یادگیری نظارت شده است: الگوریتم یادگیری معمولاً نمونه‌های آموزشی را ثابت می‌کند، بدون اینکه توانایی جستجو در برچسب نمونه‌های بدون برچسب را داشته باشد. خروجی فرضیه h مرحله ای از استقراء است. به طور کلاسیک، یک مدل استقرایی به یک مرحله آموزشی و یک مرحله کاربردی تقسیم می‌شود: پارامترهای مدل در مرحله آموزش تخمین زده می‌شوند، و مدل آموخته‌شده به صورت دلخواه بارها در مرحله کاربرد اعمال می‌شود. در حد مجانبی تعداد کاربردها، این تقسیم فازها با منابع کوانتومی نیز وجود دارد. [101]

پیاده سازی و آزمایش [ ویرایش ]

اولین آزمایش‌ها با استفاده از کامپیوتر کوانتومی موج D آدیاباتیک ، برای مثال، برای شناسایی خودروها در تصاویر دیجیتال با استفاده از تقویت منظم با تابع هدف غیرمحدب در نمایشی در سال 2009 انجام شد . شرکت های فناوری به پتانسیل یادگیری ماشین کوانتومی برای پیاده سازی های فناوری آینده علاقه نشان داده اند. در سال 2013، Google Research، ناسا و انجمن تحقیقات فضایی دانشگاه ها آزمایشگاه هوش مصنوعی کوانتومی را راه اندازی کردند که استفاده از کامپیوتر کوانتومی موج D-آدیاباتیک را بررسی می کند. [103] [104] یک مثال جدیدتر مدل‌های مولد احتمالی را با اتصال زوج دلخواه آموزش داد، که نشان می‌دهد مدل آنها قادر به تولید ارقام دست‌نویس و همچنین بازسازی تصاویر پر سر و صدا از میله‌ها و نوارها و ارقام دست‌نویس است. [63]

با استفاده از یک فناوری بازپخت متفاوت بر اساس تشدید مغناطیسی هسته‌ای (NMR)، یک شبکه کوانتومی هاپفیلد در سال 2009 اجرا شد که داده‌های ورودی و داده‌های حفظ شده را برای همیلتونی‌ها ترسیم می‌کرد و امکان استفاده از محاسبات کوانتومی آدیاباتیک را فراهم می‌کرد. [105] فناوری NMR محاسبات کوانتومی جهانی را نیز امکان‌پذیر می‌سازد، [ نیازمند منبع ] و برای اولین اجرای آزمایشی یک ماشین بردار پشتیبان کوانتومی برای تشخیص عدد دستی «6» و «9» بر روی یک کامپیوتر کوانتومی حالت مایع استفاده شد. 2015. [106] داده های آموزشی شامل پیش پردازش تصویر بود که آنها را به بردارهای 2 بعدی نرمال شده نگاشت می کرد تا تصاویر را به عنوان حالت های یک کیوبیت نشان دهد. دو ورودی بردار، نسبت عمودی و افقی شدت پیکسل تصویر است. هنگامی که بردارها در فضای ویژگی تعریف شدند ، ماشین بردار پشتیبان کوانتومی برای طبقه‌بندی بردار ورودی ناشناخته پیاده‌سازی شد. بازخوانی با خواندن وضعیت نهایی از نظر جهت (بالا/پایین) سیگنال NMR از توموگرافی کوانتومی پرهزینه جلوگیری می کند.

پیاده‌سازی فوتونیک توجه بیشتری را به خود جلب می‌کند، [107] به دلیل اینکه نیازی به خنک‌سازی گسترده ندارند. تشخیص همزمان رقم و بلندگو و پیش‌بینی سری‌های زمانی آشفته با نرخ داده‌ای بیش از 1 گیگابایت بر ثانیه در سال 2013 نشان داده شد . مرز طبقه بندی به صورت تکراری از داده های آموزشی از طریق یک قانون بازخورد. [109] یک بلوک اصلی در بسیاری از الگوریتم های یادگیری محاسبه فاصله بین دو بردار است: این اولین بار به صورت تجربی تا هشت بعد با استفاده از کیوبیت های درهم تنیده در یک کامپیوتر کوانتومی فوتونیک در سال 2015 نشان داده شد. [110]

اخیراً، بر اساس رویکرد نورومیمتیک، یک عنصر جدید به حوزه یادگیری ماشین کوانتومی اضافه شده است، در قالب یک ممریستور به اصطلاح کوانتومی، یک مدل کوانتیزه شده از ممریستور کلاسیک استاندارد . [111] این دستگاه را می‌توان با استفاده از یک مقاومت قابل تنظیم، اندازه‌گیری‌های ضعیف روی سیستم و مکانیزم پیش‌خور کلاسیک ساخت. اجرای یک ممریستور کوانتومی در مدارهای ابررسانا پیشنهاد شده است، [112] و آزمایشی با نقاط کوانتومی انجام شد. [113] یک ممریستور کوانتومی برهمکنش‌های غیرخطی را در دینامیک کوانتومی پیاده‌سازی می‌کند که به جستجوی یک شبکه عصبی کوانتومی کاملاً کاربردی کمک می‌کند.

از سال 2016، IBM یک پلت فرم آنلاین مبتنی بر ابر برای توسعه دهندگان نرم افزار کوانتومی به نام IBM Q Experience راه اندازی کرده است . این پلتفرم متشکل از چندین پردازنده کوانتومی کاملاً عملیاتی است که از طریق IBM Web API قابل دسترسی هستند. با انجام این کار، این شرکت توسعه دهندگان نرم افزار را تشویق می کند تا الگوریتم های جدید را از طریق یک محیط توسعه با قابلیت های کوانتومی دنبال کنند. معماری‌های جدید به‌صورت تجربی، تا ۳۲ کیوبیت، با استفاده از روش‌های محاسباتی کوانتومی یون به دام افتاده و ابررسانا در حال بررسی هستند.

در اکتبر 2019، اشاره شد که معرفی مولدهای اعداد تصادفی کوانتومی (QRNG) به مدل‌های یادگیری ماشین از جمله شبکه‌های عصبی و شبکه‌های عصبی کانولوشن برای توزیع وزن اولیه تصادفی و جنگل‌های تصادفی برای فرآیندهای تقسیم تأثیر عمیقی بر توانایی آنها در مقایسه با روش کلاسیک مولد اعداد شبه تصادفی (PRNGs). [114] با این حال، در یک انتشار جدیدتر از سال 2021، این ادعاها را نمی توان برای مقداردهی اولیه وزن شبکه عصبی بازتولید کرد و هیچ مزیت قابل توجهی از استفاده از QRNG ها نسبت به PRNG ها یافت نشد. [115] این کار همچنین نشان داد که تولید اعداد تصادفی منصفانه با یک کامپیوتر کوانتومی گیت یک کار غیر پیش پا افتاده در دستگاه‌های NISQ است و بنابراین استفاده از QRNG در عمل بسیار دشوارتر از PRNG است.

مقاله ای که در دسامبر 2018 منتشر شد، آزمایشی را با استفاده از یک سیستم یون به دام افتاده گزارش داد که سرعت کوانتومی زمان بررسی عوامل یادگیری تقویتی را با استفاده از سخت افزار کوانتومی داخلی نشان می دهد. [57]

در مارس 2021، تیمی از محققان از اتریش، هلند، ایالات متحده و آلمان، نمایش تجربی سرعت کوانتومی زمان یادگیری عوامل یادگیری تقویتی را گزارش کردند که به طور کامل کوانتومی با محیط تعامل دارند. [116] [58] درجات آزادی مربوط به عامل و محیط بر روی یک پردازنده نانوفوتونی یکپارچه فشرده و کاملاً قابل تنظیم تحقق یافت.

شک و تردید [ ویرایش ]

در حالی که خود یادگیری ماشین اکنون نه تنها یک زمینه تحقیقاتی است، بلکه یک صنعت مهم اقتصادی و در حال رشد سریع است و محاسبات کوانتومی یک زمینه کاملاً تثبیت شده برای تحقیقات نظری و تجربی است، یادگیری ماشین کوانتومی یک زمینه مطالعاتی صرفاً نظری باقی مانده است. تلاش برای نشان دادن تجربی مفاهیم یادگیری ماشین کوانتومی کافی نیست. [ نیازمند منبع ]

بسیاری از دانشمندان برجسته که به طور گسترده در زمینه یادگیری ماشین کوانتومی منتشر می کنند، در مورد تبلیغات گسترده در مورد این موضوع هشدار می دهند و اگر در مورد کاربردهای عملی آن در آینده قابل پیش بینی سؤال شود، بسیار خودداری می کنند. سوفیا چن [117] برخی از اظهارات دانشمندان مشهور در این زمینه را جمع آوری کرد:

فیزیکدان ماریا شولد از استارتاپ محاسبات کوانتومی کانادایی Xanadu: "من فکر می کنم ما هنوز تکالیف خود را انجام نداده ایم. این یک زمینه علمی بسیار جدید است."
هنگامی که یادگیری ماشین را با کوانتوم ترکیب می‌کنید، یک هیپ متراکم را کاتالیز می‌کنید. [118] - Jacob Biamonte یکی از همکاران در نظریه محاسبات کوانتومی.
Iordanis Kerenidis، دانشمند کامپیوتر، رئیس الگوریتم‌های کوانتومی در استارت‌آپ محاسبات کوانتومی QC Ware مبتنی بر دره سیلیکون، "کارهای زیادی وجود دارد که باید انجام شود قبل از اینکه ادعا کنیم یادگیری ماشین کوانتومی واقعا کار می‌کند."
رایان سوکه، فیزیکدان از دانشگاه آزاد برلین در آلمان، "من حتی یک مدرک ندیدم که یک کار معنی دار [یادگیری ماشینی] وجود داشته باشد که برای آن استفاده از یک کامپیوتر کوانتومی منطقی باشد نه یک کامپیوتر کلاسیک." .
"به هیاهو نخورید!" - فرانک زیکرت، [119] که نویسنده احتمالاً کاربردی ترین کتاب مرتبط با این موضوع است، مراقب باشید که "کامپیوترهای کوانتومی به دلیل توانایی بازنمایی خود از پیشرفت یادگیری ماشینی بسیار دور هستند" و حتی در مورد ارزیابی و بهینه سازی برای هر نوع کار مفید برتری کوانتومی هنوز به دست نیامده است. علاوه بر این، هیچ‌کس در میان محققین فعال در این زمینه هیچ پیش‌بینی در مورد زمان عملی شدن آن انجام نمی‌دهد. [ نیازمند منبع ]

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Quantum_machine_learning

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:19 توسط علی رضا نقش |

2-یادگیری ماشین کوانتومی

تکنیک های نمونه برداری کوانتومی [ ویرایش ]

نمونه برداری از توزیع های احتمالی با ابعاد بالا در هسته طیف گسترده ای از تکنیک های محاسباتی با کاربردهای مهم در سراسر علم، مهندسی و جامعه قرار دارد. به عنوان مثال می توان به یادگیری عمیق ، برنامه نویسی احتمالی و دیگر کاربردهای یادگیری ماشین و هوش مصنوعی اشاره کرد.

یک مشکل محاسباتی سخت، که برای برخی از وظایف یادگیری ماشین مرتبط کلیدی است، تخمین میانگین‌ها نسبت به مدل‌های احتمالی است که بر اساس توزیع بولتزمن تعریف شده‌اند . نمونه‌برداری از مدل‌های احتمالی عمومی سخت است: الگوریتم‌هایی که به شدت بر نمونه‌گیری تکیه می‌کنند، بدون توجه به اینکه منابع محاسباتی کلاسیک چقدر بزرگ و قدرتمند می‌شوند، غیرقابل حل باقی می‌مانند. حتی اگر آنیل‌کننده‌های کوانتومی، مانند آنیل‌هایی که توسط D-Wave Systems تولید می‌شوند، برای چالش‌برانگیز کردن مسائل بهینه‌سازی ترکیبی طراحی شده‌اند، اخیراً به عنوان یک نامزد بالقوه برای سرعت بخشیدن به محاسباتی که بر نمونه‌برداری با بهره‌برداری از اثرات کوانتومی متکی هستند، شناخته شده‌اند. [59]

برخی از گروه‌های تحقیقاتی اخیراً استفاده از سخت‌افزار آنیلینگ کوانتومی را برای آموزش ماشین‌های بولتزمن و شبکه‌های عصبی عمیق بررسی کرده‌اند . [60] [61] [62] رویکرد استاندارد برای آموزش ماشین‌های بولتزمن بر محاسبه میانگین‌های معینی تکیه می‌کند که می‌توان با تکنیک‌های نمونه‌گیری استاندارد ، مانند الگوریتم‌های مونت کارلو زنجیره مارکوف ، تخمین زد . امکان دیگر تکیه بر یک فرآیند فیزیکی مانند آنیل کوانتومی است که به طور طبیعی نمونه هایی از توزیع بولتزمن تولید می کند. هدف یافتن پارامترهای کنترلی بهینه است که به بهترین نحو توزیع تجربی یک مجموعه داده معین را نشان می دهد.

سیستم D-Wave 2X میزبانی شده در مرکز تحقیقات ایمز ناسا اخیراً برای یادگیری کلاس خاصی از ماشین‌های محدود شده بولتزمن استفاده شده است که می‌تواند به عنوان یک بلوک ساختمانی برای معماری‌های یادگیری عمیق عمل کند. [61] کار تکمیلی که تقریباً به طور همزمان ظاهر شد نشان داد که بازپخت کوانتومی می تواند برای یادگیری نظارت شده در وظایف طبقه بندی استفاده شود. [60] همین دستگاه بعداً برای آموزش یک ماشین بولتزمن کاملاً متصل برای تولید، بازسازی و طبقه‌بندی ارقام دست‌نویس با مقیاس پایین و با وضوح پایین، در میان سایر مجموعه‌های داده مصنوعی مورد استفاده قرار گرفت. [63] در هر دو مورد، مدل های آموزش داده شده توسط آنیل کوانتومی از نظر کیفیت عملکرد مشابه یا بهتری داشتند. سوال نهایی که این تلاش را پیش می برد این است که آیا سرعت کوانتومی در کاربردهای نمونه گیری وجود دارد یا خیر. تجربه استفاده از آنیل کوانتومی برای بهینه سازی ترکیبی نشان می دهد که پاسخ ساده نیست. بازپخت معکوس نیز برای حل یک ماشین بولتزمن محدود کوانتومی کاملا متصل استفاده شده است. [64]

با الهام از موفقیت ماشین‌های بولتزمن مبتنی بر توزیع کلاسیک بولتزمن، اخیراً یک رویکرد یادگیری ماشینی جدید مبتنی بر توزیع کوانتومی بولتزمن یک میدان عرضی Ising Hamiltonian پیشنهاد شده است. [65] به دلیل ماهیت غیر تعویضی مکانیک کوانتومی، فرآیند آموزش ماشین بولتزمن کوانتومی می‌تواند غیرمعمول شود. این مشکل، تا حدی، با معرفی محدودیت‌های احتمالات کوانتومی دور زده شد و به نویسندگان این امکان را داد که مدل را با نمونه‌گیری به طور کارآمد آموزش دهند. این امکان وجود دارد که نوع خاصی از ماشین کوانتومی بولتزمن در D-Wave 2X با استفاده از قانون یادگیری مشابه ماشین‌های بولتزمن کلاسیک آموزش دیده باشد. [63] [62] [66]

آنیل کوانتومی تنها فناوری نمونه برداری نیست. در یک سناریوی آماده سازی و اندازه گیری، یک کامپیوتر کوانتومی جهانی یک حالت حرارتی را آماده می کند که سپس با اندازه گیری ها نمونه برداری می شود. این می تواند زمان مورد نیاز برای آموزش یک ماشین بولتزمن با محدودیت عمیق را کاهش دهد و چارچوب غنی تر و جامع تری را برای یادگیری عمیق نسبت به محاسبات کلاسیک ارائه دهد. [67] همان روش‌های کوانتومی همچنین امکان آموزش کارآمد ماشین‌های بولتزمن کامل و مدل‌های چندلایه و کاملاً متصل را فراهم می‌کند و مشابه کلاسیک معروفی ندارند. با تکیه بر یک پروتکل آماده سازی حالت حرارتی کارآمد که از یک حالت دلخواه شروع می شود، شبکه های منطقی مارکوف با کوانتومی تقویت شده از تقارن ها و ساختار محلی مدل گرافیکی احتمالی تولید شده توسط یک الگوی منطقی مرتبه اول استفاده می کنند . [68] [19] این کاهش نمایی در پیچیدگی محاسباتی در استنتاج احتمالی را فراهم می‌کند، و در حالی که پروتکل به یک کامپیوتر کوانتومی جهانی متکی است، با فرضیات خفیف می‌توان آن را بر روی سخت‌افزار آنیل کوانتومی معاصر تعبیه کرد.

شبکه های عصبی کوانتومی [ ویرایش ]

مقاله اصلی: شبکه عصبی کوانتومی

آنالوگ های کوانتومی یا تعمیم شبکه های عصبی کلاسیک اغلب به عنوان شبکه های عصبی کوانتومی شناخته می شوند . این اصطلاح با طیف وسیعی از رویکردها، از جمله پیاده‌سازی و گسترش شبکه‌های عصبی با استفاده از فوتون‌ها، مدارهای متغیر لایه‌ای یا مدل‌های کوانتومی آیزینگ ادعا می‌شود. شبکه‌های عصبی کوانتومی اغلب به‌عنوان توسعه‌ای در مدل دویچ از یک شبکه محاسباتی کوانتومی تعریف می‌شوند. [69] در این مدل، دروازه‌های غیرخطی و برگشت‌ناپذیر، غیرمشابه با عملگر همیلتونی، برای حدس‌زنی مجموعه داده‌های داده‌شده مستقر می‌شوند. [69] چنین دروازه‌هایی باعث می‌شوند که فازهای خاصی قابل مشاهده نباشند و نوسانات خاصی ایجاد کنند. [69] شبکه‌های عصبی کوانتومی اطلاعات کوانتومی و محاسبات کوانتومی را در محاسبات عصبی کلاسیک به کار می‌برند. [70] تحقیقات کنونی نشان می‌دهد که QNN می‌تواند به صورت تصاعدی میزان قدرت محاسباتی و درجات آزادی را برای یک رایانه افزایش دهد، که برای رایانه‌های کلاسیک به اندازه آن محدود است. [70] یک شبکه عصبی کوانتومی دارای قابلیت های محاسباتی برای کاهش تعداد مراحل، کیوبیت های استفاده شده و زمان محاسبه است. [69] تابع موج مکانیک کوانتومی نورون شبکه های عصبی است. برای آزمایش کاربردهای کوانتومی در یک شبکه عصبی، مولکول‌های نقطه کوانتومی بر روی زیرلایه‌ای از GaAs یا موارد مشابه قرار می‌گیرند تا نحوه ارتباط آنها با یکدیگر را ثبت کنند. هر نقطه کوانتومی را می توان به عنوان جزیره ای از فعالیت الکتریکی نام برد و زمانی که چنین نقاطی به اندازه کافی نزدیک باشند (تقریباً 10 تا 20 نانومتر) [71] الکترون ها می توانند در زیر جزایر تونل بزنند. توزیع یکنواخت در سطح زیرلایه در مجموعه های دوتایی باعث ایجاد دوقطبی و در نهایت دو حالت چرخش بالا یا پایین می شود. این حالت ها معمولاً به عنوان کیوبیت با حالت های متناظر شناخته می شوند|0〉 $|0\rangle$ و|1〉 $|1\rangle$ در نماد دیراک [71]

شبکه عصبی کانولوشن کوانتومی [ ویرایش ]

یک طرح جدید برای بردارهای چند بعدی که از مدارها به عنوان فیلترهای پیچشی [72] استفاده می کند QCNN است. از مزایای CNN [73] [74] و قدرت QML الهام گرفته شد. این با استفاده از ترکیبی از یک مدار کوانتومی متغیر (VQC) [75] و یک شبکه عصبی عمیق [76] (DNN) ساخته شده است، که به طور کامل از قدرت پردازش بسیار موازی در برهم نهی یک حالت کوانتومی با تعداد محدود کیوبیت استفاده می‌کند. . استراتژی اصلی انجام یک فرآیند بهینه‌سازی تکراری در دستگاه‌های NISQ [77] ، بدون تأثیر منفی نویز، که احتمالاً در پارامتر مدار گنجانده شده است، و بدون نیاز به تصحیح خطای کوانتومی است. [78]

مدار کوانتومی باید به طور موثر اطلاعات مکانی را مدیریت کند تا QCNN به عنوان CNN عمل کند. فیلتر کانولوشن اساسی ترین تکنیک برای استفاده از اطلاعات مکانی است. یک یا چند فیلتر کانولوشن کوانتومی یک شبکه عصبی کانولوشن کوانتومی (QCNN) را تشکیل می‌دهند و هر یک از این فیلترها داده‌های ورودی را با استفاده از یک مدار کوانتومی که می‌تواند به صورت سازمان‌یافته یا تصادفی ایجاد شود، تبدیل می‌کند. سه بخش که فیلتر کانولوشن کوانتومی را تشکیل می دهند عبارتند از: رمزگذار، مدار کوانتومی پارامتری (PQC)، [79] و اندازه گیری. فیلتر کانولوشن کوانتومی را می توان به عنوان یک گسترش فیلتر در CNN سنتی مشاهده کرد زیرا با پارامترهای قابل آموزش طراحی شده است.

شبکه‌های عصبی کوانتومی از ساختارهای سلسله مراتبی بهره می‌برند، [80] و برای هر لایه بعدی، تعداد کیوبیت‌های لایه قبلی به میزان دو برابر کاهش می‌یابد. برای n کیوبیت ورودی، این ساختار دارای لایه‌های O(log(n)) هستند که امکان عمق مدار کم را فراهم می‌کند. علاوه بر این، آنها می‌توانند از «فلات بی‌ثبات»، یکی از مهم‌ترین مسائل الگوریتم‌های مبتنی بر PQC جلوگیری کنند و از قابلیت آموزش اطمینان حاصل کنند. [81] علیرغم این واقعیت که مدل QCNN شامل عملیات کوانتومی مربوطه نمی شود، ایده اساسی لایه ادغام نیز برای اطمینان از اعتبار ارائه شده است. در معماری QCNN، لایه ادغام معمولاً بین لایه‌های کانولوشنال بعدی قرار می‌گیرد. عملکرد آن کوچک کردن اندازه فضایی نمایش در عین حفظ ویژگی‌های حیاتی است که به آن اجازه می‌دهد تعداد پارامترها را کاهش دهد، محاسبات شبکه را ساده‌سازی کند و بیش از حد برازش را مدیریت کند. چنین فرآیندی را می توان با استفاده از توموگرافی کامل بر روی ایالت انجام داد تا آن را به یک کیوبیت کاهش دهد و سپس در مترو پردازش شود. متداول ترین نوع واحد مورد استفاده در لایه ادغام، حداکثر ادغام است، اگرچه انواع دیگری نیز وجود دارد. مشابه شبکه‌های عصبی پیش‌خور معمولی ، آخرین ماژول یک لایه کاملاً متصل با اتصالات کامل به تمام فعال‌سازی‌های لایه قبلی است. تغییر ناپذیری ترجمه، که به بلوک‌های یکسانی از دروازه‌های کوانتومی پارامتر شده در یک لایه نیاز دارد، یکی از ویژگی‌های متمایز معماری QCNN است. [82]

شبکه عصبی کوانتومی پراکنده [ ویرایش ]

QNN های پراکنده (DQNN) از لایه هایی از کیوبیت های جفت شده توسط پرسپترون به نام بلوک های ساختمانی ساخته می شوند که یک طرح واحد دلخواه دارند. به هر گره در لایه شبکه یک DQNN مجموعه ای مجزا از کیوبیت ها داده می شود و به هر کیوبیت نیز یک واحد پرسپترون کوانتومی واحد برای مشخص کردن آن داده می شود. [83] [84] اطلاعات حالت های ورودی از طریق شبکه به صورت پیشخور، نگاشت انتقال لایه به لایه بر روی کیوبیت های دو لایه مجاور، همانطور که از نام آن پیداست، منتقل می شود. اصطلاح Dissipative همچنین به این واقعیت اشاره دارد که لایه خروجی توسط کیوبیت های فرعی تشکیل می شود در حالی که لایه های ورودی هنگام ردیابی لایه نهایی حذف می شوند. [85] هنگام انجام یک کار یادگیری نظارت شده گسترده، از DQNN برای یادگیری یک ماتریس واحد استفاده می شود که حالت های کوانتومی ورودی و خروجی را به هم متصل می کند. داده های آموزشی برای این کار شامل حالت کوانتومی و برچسب های کلاسیک مربوطه است.

با الهام از شبکه خصمانه مولد کلاسیک بسیار موفق (GAN) ، [86] شبکه متخاصم مولد کوانتومی اتلافی (DQGAN) برای یادگیری بدون نظارت داده های آموزشی بدون برچسب معرفی شده است. مولد و متمایز کننده دو DQNN هستند که یک DQGAN را تشکیل می دهند. [84] هدف مولد ایجاد حالت‌های آموزشی نادرست است که تمایزکننده نمی‌تواند آن‌ها را از حالت‌های واقعی متمایز کند، در حالی که هدف تمایزکننده این است که حالت‌های آموزشی واقعی را از حالت‌های جعلی ایجاد شده توسط مولد جدا کند. ویژگی‌های مربوط به مجموعه آموزشی توسط مولد توسط آموزش متناوب و متخاصم شبکه‌ها که به تولید مجموعه‌هایی که مجموعه آموزشی را گسترش می‌دهند، یاد می‌گیرد. DQGAN یک معماری کاملا کوانتومی دارد و در داده های کوانتومی آموزش دیده است.

مدل‌های مارکوف کوانتومی پنهان [ ویرایش ]

مدل‌های مارکوف کوانتومی پنهان [87] (HQMMs) یک نسخه بهبود یافته کوانتومی از مدل‌های کلاسیک مارکوف پنهان (HMMs) هستند که معمولاً برای مدل‌سازی داده‌های متوالی در زمینه‌های مختلف مانند روباتیک و پردازش زبان طبیعی استفاده می‌شوند . برخلاف رویکرد دیگر الگوریتم‌های یادگیری ماشین پیشرفته کوانتومی، HQMM ها را می‌توان به عنوان مدل‌هایی الهام‌گرفته از مکانیک کوانتومی در نظر گرفت که می‌توانند روی رایانه‌های کلاسیک نیز اجرا شوند. [88] در جایی که HMM های کلاسیک از بردارهای احتمال برای نمایش حالت های «باور» پنهان استفاده می کنند، HQMM ها از آنالوگ کوانتومی استفاده می کنند: ماتریس های چگالی . کار اخیر نشان داده است که این مدل‌ها را می‌توان با بهینه‌سازی کلاسیک به‌طور موفقیت‌آمیز یاد گرفت، و شواهد تجربی وجود دارد مبنی بر اینکه این مدل‌ها می‌توانند داده‌های متوالی را در مقایسه با HMM‌های کلاسیک در عمل مدل‌سازی کنند، اگرچه کار بیشتر در این زمینه انجام می‌شود. برای تعیین دقیق زمان و چگونگی به دست آوردن این مزایا مورد نیاز است. [88] علاوه بر این، از آنجایی که HMM های کلاسیک نوع خاصی از شبکه بیز هستند ، یک جنبه هیجان انگیز از HQMM ها این است که تکنیک های مورد استفاده نشان می دهد که چگونه می توانیم استنتاج بیزی مشابه کوانتومی را انجام دهیم ، که باید امکان ساخت کلی نسخه های کوانتومی احتمالات را فراهم کند. مدل های گرافیکی [88]

یادگیری ماشین کاملاً کوانتومی [ ویرایش ]

در کلی‌ترین حالت یادگیری ماشین کوانتومی، هم دستگاه یادگیری و هم سیستم مورد مطالعه و همچنین تعامل آنها کاملاً کوانتومی هستند. در این بخش چند نمونه از نتایج در مورد این موضوع ارائه می شود.

یک دسته از مشکلاتی که می‌تواند از رویکرد کاملاً کوانتومی سود ببرد، «یادگیری» حالات، فرآیندها یا اندازه‌گیری‌های کوانتومی ناشناخته است، به این معنا که می‌توان آنها را متعاقباً در یک سیستم کوانتومی دیگر بازتولید کرد. برای مثال، ممکن است کسی بخواهد اندازه‌گیری را یاد بگیرد که بین دو حالت منسجم تمایز قائل شود، نه با توجه به توصیف کلاسیک حالت‌هایی که باید متمایز شوند، بلکه در عوض مجموعه‌ای از نمونه‌های سیستم‌های کوانتومی آماده‌شده در این حالت‌ها را در نظر می‌گیریم. رویکرد ساده لوحانه ابتدا استخراج یک توصیف کلاسیک از حالات و سپس اجرای یک اندازه گیری تمایزآمیز ایده آل بر اساس این اطلاعات است. این فقط به یادگیری کلاسیک نیاز دارد. با این حال، می توان نشان داد که یک رویکرد کاملا کوانتومی در این مورد به شدت برتر است. [89] (این همچنین به کار بر روی تطبیق الگوی کوانتومی مربوط می‌شود. [90] ) مسئله یادگیری تبدیل‌های واحد را می‌توان به روشی مشابه مورد بررسی قرار داد. [91]

فراتر از مشکل خاص یادگیری حالات و تبدیل ها، وظیفه خوشه بندی یک نسخه کاملاً کوانتومی را نیز می پذیرد، که در آن هم اوراکل که فاصله بین نقاط داده را برمی گرداند و هم دستگاه پردازش اطلاعاتی که الگوریتم را اجرا می کند، کوانتومی هستند. [92] در نهایت، یک چارچوب کلی شامل یادگیری نظارت شده، بدون نظارت و تقویتی در تنظیمات کاملاً کوانتومی معرفی شد، [29] که در آن همچنین نشان داده شد که امکان بررسی محیط در برهم‌نهی‌ها امکان افزایش سرعت کوانتومی در یادگیری تقویتی را فراهم می‌کند. چنین سرعت بخشی در الگوی یادگیری تقویتی به طور تجربی در یک تنظیم فوتونیک نشان داده شده است. [58]

یادگیری ماشین کوانتومی قابل توضیح [ ویرایش ]

نیاز به مدل هایی که برای انسان قابل درک باشد در یادگیری ماشین کوانتومی در قیاس با یادگیری ماشین کلاسیک ظاهر می شود و زمینه تحقیقاتی یادگیری ماشین کوانتومی قابل توضیح (یا XQML [93] در قیاس با XAI/XML ) را هدایت می کند. XQML را می توان به عنوان یک جهت تحقیق جایگزین به جای یافتن مزیت کوانتومی در نظر گرفت. [94] برای مثال، XQML در زمینه شناسایی و طبقه بندی بدافزار موبایل استفاده شده است. [95] مقادیر کوانتومی شیپلی نیز برای تفسیر دروازه‌های درون مدار بر اساس رویکرد نظری بازی پیشنهاد شده‌اند. [93] برای این منظور، دروازه‌ها به جای ویژگی‌ها به عنوان بازیکن در یک بازی ائتلافی با تابع مقداری که به اندازه‌گیری مدار کوانتومی مورد نظر بستگی دارد، عمل می‌کنند.

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:18 توسط علی رضا نقش |

1-یادگیری ماشین کوانتومی

از ویکیپدیا، دانشنامه آزاد

به نظر می رسد یکی از مشارکت کنندگان اصلی این مقاله ارتباط نزدیکی با موضوع آن داشته باشد. ممکن است برای مطابقت با خط‌مشی‌های محتوای ویکی‌پدیا، به‌ویژه دیدگاه خنثی ، نیاز به پاک‌سازی داشته باشد . لطفاً در صفحه بحث بیشتر بحث کنید . ( سپتامبر 2018 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

این مقاله ممکن است نیاز به بازنویسی داشته باشد تا با استانداردهای کیفیت ویکی‌پدیا مطابقت داشته باشد . شما می توانید کمک کنید . شاید صفحه گفتگو شامل پیشنهاداتی باشد. ( ژوئیه 2023 )

مکانیک کوانتومی
بخشی از مجموعه مقالات در مورد
منℏ∂∂تی\|�(تی)〉=اچ^\|�(تی)〉 $i\hbar {\frac {\partial }{\partial t}}\|\psi (t)\rangle ={\hat {H}}\|\psi (t)\rangle$ معادله شرودینگر
معرفی واژه نامه تاریخ
نشان می دهد زمینه
نشان می دهد مبانی
نشان می دهد آزمایش
نشان می دهد فرمولاسیون
نشان می دهد معادلات
نشان می دهد تفاسیر
نشان می دهد موضوعات پیشرفته
نشان می دهد دانشمندان
v تی ه

یادگیری ماشین کوانتومی ادغام الگوریتم های کوانتومی در برنامه های یادگیری ماشین است . [1] [2] [3] [4] [5] [6] [7] [8]

رایج ترین استفاده از این اصطلاح به الگوریتم های یادگیری ماشین برای تجزیه و تحلیل داده های کلاسیک اجرا شده بر روی یک کامپیوتر کوانتومی اشاره دارد ، یعنی یادگیری ماشین با کوانتومی پیشرفته. [9] [10] [11] در حالی که الگوریتم‌های یادگیری ماشین برای محاسبه مقادیر بسیار زیاد داده استفاده می‌شوند، یادگیری ماشین کوانتومی از کیوبیت‌ها و عملیات کوانتومی یا سیستم‌های کوانتومی تخصصی برای بهبود سرعت محاسباتی و ذخیره داده‌ها توسط الگوریتم‌ها در یک برنامه استفاده می‌کند. [12] این شامل روش‌های ترکیبی می‌شود که شامل پردازش کلاسیک و کوانتومی می‌شود، جایی که برنامه‌های فرعی سخت محاسباتی به یک دستگاه کوانتومی برون‌سپاری می‌شوند. [13] [14] [15] این روال‌ها می‌توانند ماهیت پیچیده‌تری داشته باشند و در یک کامپیوتر کوانتومی سریع‌تر اجرا شوند. [7] علاوه بر این، الگوریتم‌های کوانتومی را می‌توان برای تحلیل حالت‌های کوانتومی به جای داده‌های کلاسیک استفاده کرد. [16] [17]

فراتر از محاسبات کوانتومی، اصطلاح «یادگیری ماشین کوانتومی» با روش‌های یادگیری ماشین کلاسیک نیز مرتبط است که برای داده‌های تولید شده از آزمایش‌های کوانتومی (یعنی یادگیری ماشینی سیستم‌های کوانتومی )، مانند یادگیری انتقال فاز یک سیستم کوانتومی استفاده می‌شود [18] [19 ]. ] یا ایجاد آزمایش های کوانتومی جدید. [20] [21] [22]

یادگیری ماشین کوانتومی همچنین به شاخه ای از تحقیقات گسترش می یابد که شباهت های روش شناختی و ساختاری بین سیستم های فیزیکی خاص و سیستم های یادگیری، به ویژه شبکه های عصبی را بررسی می کند. به عنوان مثال، برخی از تکنیک های ریاضی و عددی از فیزیک کوانتومی برای یادگیری عمیق کلاسیک و بالعکس قابل استفاده هستند. [23] [24] [25]

علاوه بر این، محققان مفاهیم انتزاعی بیشتری از نظریه یادگیری را با توجه به اطلاعات کوانتومی، که گاهی اوقات به عنوان "نظریه یادگیری کوانتومی" نامیده می شود، بررسی می کنند. [26] [27]

چهار رویکرد مختلف برای ترکیب رشته‌های محاسبات کوانتومی و یادگیری ماشین. [28] [29] حرف اول به کلاسیک یا کوانتومی بودن سیستم مورد مطالعه اشاره دارد، در حالی که حرف دوم مشخص می کند که آیا یک دستگاه پردازش اطلاعات کلاسیک یا کوانتومی استفاده می شود.

یادگیری ماشین با کامپیوترهای کوانتومی [ ویرایش ]

یادگیری ماشینی پیشرفته کوانتومی به الگوریتم‌های کوانتومی اشاره دارد که وظایف را در یادگیری ماشین حل می‌کند و در نتیجه تکنیک‌های یادگیری ماشین کلاسیک را بهبود می‌بخشد و اغلب تسریع می‌کند. چنین الگوریتم‌هایی معمولاً نیازمند کدگذاری مجموعه داده‌های کلاسیک در یک کامپیوتر کوانتومی هستند تا برای پردازش اطلاعات کوانتومی قابل دسترسی باشد. متعاقباً، روال‌های پردازش اطلاعات کوانتومی اعمال می‌شوند و نتیجه محاسبات کوانتومی با اندازه‌گیری سیستم کوانتومی خوانده می‌شود. به عنوان مثال، نتیجه اندازه گیری یک کیوبیت، نتیجه یک کار طبقه بندی باینری را نشان می دهد. در حالی که بسیاری از پیشنهادات الگوریتم‌های یادگیری ماشین کوانتومی هنوز کاملاً تئوری هستند و برای آزمایش به یک کامپیوتر کوانتومی جهانی در مقیاس کامل نیاز دارند ، برخی دیگر بر روی دستگاه‌های کوانتومی در مقیاس کوچک یا با هدف خاص پیاده‌سازی شده‌اند.

حافظه های انجمنی کوانتومی و تشخیص الگوی کوانتومی [ ویرایش ]

انجمنی (یا خاطرات آدرس‌پذیر محتوا) می‌توانند محتوای ذخیره‌شده را بر اساس معیار تشابه تشخیص دهند، نه آدرس‌های ثابت، مانند حافظه‌های دسترسی تصادفی. به این ترتیب، آنها باید بتوانند الگوهای ناقص و خراب را بازیابی کنند، وظیفه اصلی یادگیری ماشین در تشخیص الگو.

حافظه های انجمنی کلاسیک معمولی الگوهای p را در حافظه ذخیره می کنند�(�2) $O(n^{2})$ فعل و انفعالات (سیناپس) یک ماتریس انرژی واقعی و متقارن بر روی شبکه ای از n نورون مصنوعی. کدگذاری به گونه‌ای است که الگوهای مورد نظر حداقل‌های محلی انرژی عملکردی هستند و بازیابی با به حداقل رساندن انرژی کل انجام می‌شود و از یک پیکربندی اولیه شروع می‌شود.

متأسفانه، خاطرات تداعی کلاسیک به شدت توسط پدیده گفتگوی متقابل محدود شده است. هنگامی که الگوهای زیادی ذخیره می شوند، خاطرات جعلی ظاهر می شوند که به سرعت تکثیر می شوند، به طوری که چشم انداز انرژی نامنظم می شود و دیگر امکان بازیابی وجود ندارد. تعداد الگوهای قابل ذخیره معمولاً توسط یک تابع خطی از تعداد نورون ها محدود می شود.پ≤�(�) $p\leq O(n)$ .

خاطرات تداعی کوانتومی [2] [3] [4] (در ساده ترین شکل ممکن) الگوها را در یک ماتریس واحد U ذخیره می کند که بر روی فضای هیلبرت n کیوبیتی عمل می کند. بازیابی با تکامل واحد از یک حالت اولیه ثابت به یک برهم نهی کوانتومی از الگوهای مورد نظر با توزیع احتمال به اوج خود در شبیه ترین الگوی به ورودی تحقق می یابد. بنابراین، فرآیند بازیابی به دلیل ماهیت کوانتومی خود احتمالی است. از آنجایی که حافظه‌های تداعی کوانتومی عاری از گفتگو هستند، حافظه‌های جعلی هرگز تولید نمی‌شوند. به همین ترتیب، آنها ظرفیت برتری نسبت به کلاسیک دارند. تعداد پارامترهای ماتریس واحد U است�(پ�) $O(pn)$ . بنابراین می‌توان حافظه‌های ارتباطی کوانتومی کارآمد و بدون حافظه کاذب را برای هر تعداد چند جمله‌ای از الگوها داشت.

شبیه سازی جبر خطی با دامنه های کوانتومی [ ویرایش ]

تعدادی از الگوریتم‌های کوانتومی برای یادگیری ماشین مبتنی بر ایده رمزگذاری دامنه هستند، یعنی ارتباط دادن دامنه‌های یک حالت کوانتومی با ورودی‌ها و خروجی‌های محاسبات. [30] [31] [32] از آنجایی که یک حالت� $n$ کیوبیت توسط2� $2^{n}$ دامنه های پیچیده، این رمزگذاری اطلاعات می تواند یک نمایش فشرده را به صورت نمایی امکان پذیر کند. به طور شهودی، این مربوط به ارتباط یک توزیع احتمال گسسته بر روی متغیرهای تصادفی باینری با یک بردار کلاسیک است. هدف الگوریتم‌های مبتنی بر رمزگذاری دامنه، فرمول‌بندی الگوریتم‌های کوانتومی است که منابع آنها به صورت چندجمله‌ای در تعداد کیوبیت‌ها رشد می‌کنند.� $n$ ، که به پیچیدگی زمانی لگاریتمی در تعداد دامنه ها و در نتیجه بعد ورودی می رسد.

بسیاری از الگوریتم‌های یادگیری ماشین کوانتومی در این دسته بر اساس تغییرات الگوریتم کوانتومی برای سیستم‌های معادلات خطی [33] (به‌عنوان محاوره‌ای HHL، به نام نویسندگان مقاله) که تحت شرایط خاص، وارونگی ماتریس را با استفاده از مقداری منابع فیزیکی انجام می‌دهند، هستند. تنها به صورت لگاریتمی در ابعاد ماتریس رشد می کند. یکی از این شرایط این است که یک همیلتونی که از نظر ورودی با ماتریس مطابقت دارد، می تواند به طور موثر شبیه سازی شود، که اگر ماتریس پراکنده باشد [34] یا رتبه پایین، ممکن است. [35] برای مرجع، هر الگوریتم کلاسیک شناخته شده برای وارونگی ماتریس به تعدادی عملیات نیاز دارد که بیش از درجه دوم در بعد ماتریس رشد می کند (مثلا�(�2.373) $O{\mathord {\left(n^{2.373}\right)}}$ ، اما آنها به ماتریس های پراکنده محدود نمی شوند.

وارونگی ماتریس کوانتومی را می توان برای روش های یادگیری ماشین اعمال کرد که در آن آموزش به حل یک سیستم خطی معادلات کاهش می یابد ، به عنوان مثال در رگرسیون خطی حداقل مربعات، [31] [32] نسخه حداقل مربعات ماشین های بردار پشتیبان ، [30] ] و فرآیندهای گاوسی. [36]

یکی از گلوگاه‌های مهم روش‌هایی که محاسبات جبر خطی را با دامنه‌های حالت‌های کوانتومی شبیه‌سازی می‌کنند، آماده‌سازی حالت است، که اغلب نیاز به مقداردهی اولیه یک سیستم کوانتومی در حالتی دارد که دامنه‌های آن منعکس‌کننده ویژگی‌های کل مجموعه داده است. اگرچه روش های کارآمد برای آماده سازی حالت برای موارد خاص شناخته شده است، [37] [38] این مرحله به راحتی پیچیدگی کار را پنهان می کند. [39] [40]

الگوریتم های کوانتومی متغیر (VQAs) [ ویرایش ]

VQAها یکی از الگوریتم‌های کوانتومی هستند که بیشتر مورد مطالعه قرار گرفته‌اند، زیرا محققان انتظار دارند که تمام برنامه‌های کاربردی مورد نیاز برای رایانه‌های کوانتومی از VQAها استفاده کنند و همچنین به نظر می‌رسد که VQAها انتظارات برای کسب برتری کوانتومی را برآورده می‌کنند. VQAs یک رویکرد ترکیبی کوانتومی-کلاسیک است که در آن پردازنده کوانتومی حالت‌های کوانتومی را آماده می‌کند و اندازه‌گیری انجام می‌شود و بهینه‌سازی توسط یک کامپیوتر کلاسیک انجام می‌شود. VQA ها برای NISQ بهترین در نظر گرفته می شوند زیرا VQA ها نسبت به سایر الگوریتم ها نسبت به سایر الگوریتم ها مقاوم به نویز هستند و تنها با چند صد کیوبیت برتری کوانتومی را به ارمغان می آورند. محققان الگوریتم‌های مبتنی بر مدار را برای حل مسائل بهینه‌سازی و یافتن انرژی حالت پایه سیستم‌های پیچیده مورد مطالعه قرار داده‌اند، که حل آن‌ها دشوار بود یا برای انجام محاسبات با استفاده از رایانه کلاسیک به زمان زیادی نیاز داشت. [41] [42]

مدارهای کوانتومی متغیر (VQCs) [ ویرایش ]

مدارهای کوانتومی متغیر که به عنوان مدارهای کوانتومی پارامتریزه شده (PQC) نیز شناخته می شوند، بر اساس الگوریتم های کوانتومی متغیر (VQA) هستند. VQC ها از سه بخش، آماده سازی حالت های اولیه، مدار کوانتومی و اندازه گیری تشکیل شده اند. محققان به طور گسترده در حال مطالعه VQC ها هستند، زیرا از قدرت محاسبات کوانتومی برای یادگیری در زمان کوتاه استفاده می کند و همچنین از پارامترهای کمتری نسبت به همتایان کلاسیک خود استفاده می کند. از نظر تئوری و عددی ثابت شده است که می‌توانیم توابع غیرخطی، مانند توابع مورد استفاده در شبکه‌های عصبی، در مدارهای کوانتومی را تقریب بزنیم. به دلیل برتری VQCها، شبکه عصبی با VQCها در وظایف یادگیری تقویتی و الگوریتم های مولد جایگزین شده است. ماهیت ذاتی دستگاه‌های کوانتومی نسبت به عدم پیوستگی، خطای دروازه تصادفی و خطاهای اندازه‌گیری باعث شده است که پتانسیل بالایی برای محدود کردن آموزش مدارهای تغییرات داشته باشند. آموزش VQC ها بر روی دستگاه های کلاسیک قبل از استفاده از آنها در دستگاه های کوانتومی به غلبه بر مشکل نویز ناهمدوسی که از طریق تعداد تکرارها برای آموزش ایجاد می شود، کمک می کند. [43] [44] [45]

طبقه بندی کننده باینری کوانتومی [ ویرایش ]

سازماندهی مجدد الگو یکی از وظایف مهم یادگیری ماشینی است، طبقه بندی باینری یکی از ابزارها یا الگوریتم های یافتن الگوها است. طبقه بندی باینری در یادگیری نظارت شده و در یادگیری بدون نظارت استفاده می شود . در یادگیری ماشین کوانتومی، بیت‌های کلاسیک به کیوبیت تبدیل می‌شوند و به فضای هیلبرت نگاشت می‌شوند. برای استفاده از مزیت فضای هیلبرت، از داده‌های مقادیر پیچیده در طبقه‌بندی‌کننده باینری کوانتومی استفاده می‌شود. [46] [47] با بهره‌برداری از ویژگی‌های مکانیک کوانتومی مانند برهم‌نهی، درهم‌تنیدگی، تداخل، طبقه‌بندی‌کننده دوتایی کوانتومی نتیجه دقیق را در مدت زمان کوتاهی تولید می‌کند. [48]

الگوریتم های یادگیری ماشین کوانتومی بر اساس جستجوی گروور [ ویرایش ]

روش دیگری برای بهبود یادگیری ماشین کلاسیک با پردازش اطلاعات کوانتومی از روش‌های تقویت دامنه مبتنی بر الگوریتم جستجوی گروور استفاده می‌کند که نشان داده شده است که مشکلات جستجوی بدون ساختار را با سرعت دوم در مقایسه با الگوریتم‌های کلاسیک حل می‌کند. این روال‌های کوانتومی را می‌توان برای الگوریتم‌های یادگیری که به یک کار جستجوی ساختاریافته تبدیل می‌شوند، به کار برد، همانطور که می‌توان برای مثال در مورد k -medias [49] و الگوریتم‌های k-نزدیک‌ترین همسایه‌ها انجام داد . [9] کاربرد دیگر افزایش سرعت درجه دوم در آموزش پرسپترون است . [50]

نمونه ای از تقویت دامنه که در الگوریتم یادگیری ماشین استفاده می شود، کمینه سازی الگوریتم جستجوی گروور است. که در آن یک زیربرنامه از الگوریتم جستجوی گروور برای یافتن عنصری کمتر از برخی از عناصر تعریف شده قبلی استفاده می کند. این را می توان با یک اوراکل انجام داد که تعیین می کند آیا یک حالت با عنصر مربوطه کمتر از حالت از پیش تعریف شده است یا خیر. سپس الگوریتم گروور می تواند عنصری را پیدا کند که شرط ما برآورده شود. کمینه سازی توسط برخی از عناصر تصادفی در مجموعه داده ما مقداردهی اولیه می شود و به طور مکرر این زیر روال را برای یافتن حداقل عنصر در مجموعه داده انجام می دهد. این کمینه سازی به طور قابل توجهی در میانه های k کوانتومی استفاده می شود و حداقل سرعت آن افزایش می یابد�(�/ک) $O({\sqrt {n/k}})$ در مقایسه با نسخه های کلاسیک k-medias، که در آن� $n$ تعداد نقاط داده وک $k$ تعداد خوشه ها است. [49]

تقویت دامنه اغلب با راه رفتن کوانتومی ترکیب می شود تا به همان سرعت درجه دوم برسد. پیاده‌روی‌های کوانتومی برای بهبود الگوریتم رتبه صفحه گوگل [51] و همچنین عملکرد عوامل یادگیری تقویتی در چارچوب شبیه‌سازی تصویری پیشنهاد شده‌اند. [52]

یادگیری تقویتی کوانتومی [ ویرایش ]

یادگیری تقویتی شاخه ای از یادگیری ماشینی است که از یادگیری تحت نظارت و بدون نظارت متمایز است، که پیشرفت های کوانتومی را نیز می پذیرد. [53] [52] [54] در یادگیری تقویت شده کوانتومی، یک عامل کوانتومی با یک محیط کلاسیک یا کوانتومی در تعامل است و گهگاه برای اعمال خود پاداش دریافت می کند، که به عامل اجازه می دهد رفتار خود را تطبیق دهد - به عبارت دیگر، یاد بگیرد که چه چیزی انجام دهید تا پاداش بیشتری کسب کنید. در برخی شرایط، یا به دلیل قابلیت پردازش کوانتومی عامل، [52] یا به دلیل امکان بررسی محیط در برهم نهی ها ، [29] ممکن است یک سرعت کوانتومی حاصل شود. پیاده سازی این نوع پروتکل ها برای سیستم های یون های به دام افتاده [55] و مدارهای ابررسانا پیشنهاد شده است . [56] سرعت کوانتومی زمان تصمیم گیری داخلی عامل [52] به طور تجربی در یون های به دام افتاده نشان داده شده است، [57] در حالی که سرعت کوانتومی زمان یادگیری در یک برهمکنش کاملا منسجم (کوانتومی) بین عامل و محیط به طور تجربی در یک تنظیم فوتونیک تحقق یافته است. [58]

آنیل کوانتومی [ ویرایش ]

مقاله اصلی: آنیل کوانتومی

بازپخت کوانتومی یک تکنیک بهینه‌سازی است که برای تعیین مینیمم و ماکزیمم محلی یک تابع در مجموعه معینی از توابع کاندید استفاده می‌شود. این روشی برای گسسته کردن یک تابع با مینیمم ها یا ماکزیمم های محلی فراوان به منظور تعیین قابل مشاهده های تابع است. این فرآیند را می توان از بازپخت شبیه سازی شده توسط فرآیند تونل زنی کوانتومی متمایز کرد ، که توسط آن ذرات از طریق موانع جنبشی یا بالقوه از حالت بالا به حالت پایین تونل می زنند. بازپخت کوانتومی از برهم نهی همه حالات ممکن یک سیستم با وزن مساوی شروع می شود. سپس معادله شرودینگر وابسته به زمان، تکامل زمانی سیستم را هدایت می‌کند و با افزایش زمان، دامنه هر حالت را تحت تأثیر قرار می‌دهد. در نهایت، می توان به حالت پایه رسید تا همیلتونی آنی سیستم را به دست آورد.

مدار NISQ به عنوان مدل کوانتومی [ ویرایش ]

با پیشروی عمق مدار کوانتومی در دستگاه‌های NISQ ، سطح نویز افزایش می‌یابد و چالش قابل‌توجهی را برای محاسبه دقیق هزینه‌ها و گرادیان‌ها در مدل‌های آموزشی ایجاد می‌کند. تحمل نویز با استفاده از پرسپترون کوانتومی و الگوریتم کوانتومی در سخت‌افزار کوانتومی در دسترس بهبود می‌یابد. [ نیازمند منبع ]

اتصال منظم اجزای مشابهی که به عنوان نورون ها شناخته می شوند ، اساس حتی پیچیده ترین شبکه های مغزی را تشکیل می دهد. به طور معمول، یک نورون دو عملیات دارد: محصول داخلی و یک تابع فعال سازی . برخلاف تابع فعال‌سازی، که معمولاً غیرخطی است ، محصول داخلی یک فرآیند خطی است. با محاسبات کوانتومی، فرآیندهای خطی ممکن است به راحتی انجام شوند، به دلیل سادگی اجرا، تابع آستانه توسط اکثر نورون‌های کوانتومی برای توابع فعال‌سازی ترجیح داده می‌شود. [ نیازمند منبع ]

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:15 توسط علی رضا نقش |

1-محاسبات غیر متعارف

محاسبات غیر متعارف محاسبه با هر یک از طیف گسترده ای از روش های جدید یا غیر معمول است . به عنوان محاسبات جایگزین نیز شناخته می شود .

اصطلاح محاسبات غیر متعارف توسط کریستین اس. کالود و جان کستی ابداع شد و در اولین کنفرانس بین المللی مدل های غیر متعارف محاسبات [1] در سال 1998 مورد استفاده قرار گرفت .

پس زمینه [ ویرایش ]

تئوری کلی محاسبات امکان مدل‌های مختلفی را می‌دهد. [ توضیحات لازم ] فن آوری محاسبات ابتدا با استفاده از سیستم های مکانیکی توسعه یافت و سپس به استفاده از دستگاه های الکترونیکی تبدیل شد. سایر زمینه های فیزیک مدرن راه های بیشتری برای توسعه فراهم می کنند.

مدل محاسباتی [ ویرایش ]

مقاله اصلی: مدل محاسباتی

مدل‌های محاسباتی از برنامه‌های کامپیوتری برای شبیه‌سازی و مطالعه سیستم‌های پیچیده با استفاده از رویکرد الگوریتمی یا مکانیکی استفاده می‌کنند. آنها معمولا برای مطالعه سیستم های غیرخطی پیچیده ای که راه حل های تحلیلی ساده به راحتی در دسترس نیستند استفاده می شوند. [3] آزمایش با مدل با تنظیم پارامترها در رایانه و مطالعه تفاوت‌ها در نتیجه انجام می‌شود. [4] نظریه‌های عملیاتی مدل را می‌توان از این آزمایش‌های محاسباتی استخراج یا استنباط کرد. نمونه هایی از مدل های محاسباتی شامل مدل های پیش بینی آب و هوا، مدل های شبیه ساز زمین، مدل های شبیه ساز پرواز، مدل های تاشو پروتئین مولکولی و مدل های شبکه عصبی می باشد.

محاسبات مکانیکی [ ویرایش ]

مقاله اصلی: کامپیوتر مکانیکی

هامان مانوس آر، یک کامپیوتر مکانیکی

از نظر تاریخی، کامپیوترهای مکانیکی قبل از ظهور ترانزیستور در صنعت استفاده می شدند .

امروزه کامپیوترهای مکانیکی، هم در تحقیقات و هم به عنوان کامپیوترهای آنالوگ، علاقه خود را حفظ کرده اند. برخی از رایانه‌های مکانیکی ارتباط نظری یا آموزشی دارند، مانند رایانه‌های توپ بیلیارد ، در حالی که رایانه‌های هیدرولیک مانند MONIAC یا ادغام‌کننده آب به طور مؤثر استفاده می‌شوند. [5]

در حالی که برخی در واقع شبیه سازی شده اند، برخی دیگر [ توضیحات لازم است ] . هیچ تلاشی [ مشکوک - بحث ] برای ساخت یک کامپیوتر کارآمد از طریق برخوردهای مکانیکی توپ های بیلیارد انجام نشده است. کامپیوتر دومینو یکی دیگر از طرح‌های محاسباتی مکانیکی جالب نظری است. [ چرا؟ ]

محاسبات آنالوگ [ ویرایش ]

مقاله اصلی: کامپیوتر آنالوگ

چرتکه ، نوعی کامپیوتر مکانیکی .

کامپیوتر آنالوگ نوعی کامپیوتر است که از سیگنال های آنالوگ که کمیت های فیزیکی پیوسته هستند برای مدل سازی و حل مسائل استفاده می کند. این سیگنال ها می توانند ماهیت الکتریکی ، مکانیکی یا هیدرولیکی داشته باشند. کامپیوترهای آنالوگ به طور گسترده در کاربردهای علمی و صنعتی مورد استفاده قرار می گرفتند و در آن زمان اغلب سریعتر از کامپیوترهای دیجیتال بودند. با این حال، آنها در دهه 1950 و 1960 شروع به منسوخ شدن کردند و اکنون بیشتر در کاربردهای خاص مانند شبیه سازهای پرواز هواپیما و سیستم های کنترل تدریس در دانشگاه ها استفاده می شوند. [6] نمونه‌هایی از دستگاه‌های محاسباتی آنالوگ شامل قوانین اسلاید ، نوموگرام‌ها و مکانیسم‌های پیچیده برای کنترل فرآیند و رله‌های حفاظتی است. [7] مکانیسم Antikythera ، یک دستگاه مکانیکی که موقعیت سیارات و ماه را محاسبه می‌کند، و پلان متر ، یکپارچه‌کننده مکانیکی برای محاسبه مساحت یک شکل دو بعدی دلخواه، نیز نمونه‌هایی از محاسبات آنالوگ هستند.

کامپیوترهای دیجیتال الکترونیکی [ ویرایش ]

اکثر رایانه‌های مدرن رایانه‌های الکترونیکی با معماری فون نویمان مبتنی بر الکترونیک دیجیتال هستند که با ادغام گسترده‌ای که پس از اختراع ترانزیستور و مقیاس‌بندی قانون مور امکان‌پذیر شد .

محاسبات غیر متعارف بر اساس [ کدام؟ توضیحات کنفرانس، [ 8] "یک حوزه تحقیقاتی میان رشته ای با هدف اصلی غنی سازی یا فراتر رفتن از مدل های استاندارد، مانند معماری کامپیوتر فون نویمان و ماشین تورینگ ، که بیش از نیم قرن بر علم کامپیوتر تسلط داشته اند". این روش ها عملیات محاسباتی خود را بر اساس پارادایم های غیر استاندارد مدل می کنند و در حال حاضر بیشتر در مرحله تحقیق و توسعه هستند.

این رفتار محاسباتی را می‌توان با استفاده از میکرو ترانزیستورهای کلاسیک مبتنی بر سیلیکون یا فناوری‌های محاسباتی حالت جامد «شبیه‌سازی» [ توضیحات لازم ] انجام داد ، اما هدف آن دستیابی به نوع جدیدی از محاسبات است.

رویکردهای عمومی [ ویرایش ]

اینها نمونه های غیر شهودی و آموزشی هستند که نشان می دهد یک کامپیوتر تقریباً از هر چیزی ساخته می شود.

اشیاء فیزیکی [ ویرایش ]

مقالات اصلی: کامپیوتر توپ بیلیارد و کامپیوتر دومینو

یک دروازه OR که از دومینو ساخته شده است

کامپیوتر توپ بیلیارد نوعی کامپیوتر مکانیکی است که از حرکت توپ های کروی بیلیارد برای انجام محاسبات استفاده می کند. در این مدل، سیم‌های مدار بولی با مسیرهایی برای حرکت توپ‌ها نشان داده می‌شوند، وجود یا عدم وجود توپ در یک مسیر سیگنال روی آن سیم را رمزگذاری می‌کند و دروازه‌ها با برخورد توپ‌ها در نقاطی شبیه‌سازی می‌شوند. مسیرها متقاطع می شوند [9] [10]

کامپیوتر دومینو یک کامپیوتر مکانیکی است که از دومینوهای ایستاده برای نشان دادن تقویت یا دروازه منطقی سیگنال های دیجیتال استفاده می کند. از این ساختارها می توان برای نشان دادن مفاهیم دیجیتالی و حتی برای ساخت ماژول های پردازش اطلاعات ساده استفاده کرد. [11] [12]

کامپیوترهای توپ بیلیارد و کامپیوترهای دومینو نمونه‌هایی از روش‌های محاسباتی غیر متعارف هستند که از اشیاء فیزیکی برای انجام محاسبات استفاده می‌کنند.

محاسبات مخزن [ ویرایش ]

مقاله اصلی: محاسبات مخزن

محاسبات مخزن یک چارچوب محاسباتی برگرفته از نظریه شبکه عصبی مکرر است که شامل نگاشت سیگنال های ورودی به فضاهای محاسباتی با ابعاد بالاتر از طریق دینامیک یک سیستم ثابت و غیر خطی به نام مخزن است. مخزن، که می تواند مجازی یا فیزیکی باشد، از واحدهای غیرخطی مجزا تشکیل شده است که در حلقه های مکرر به هم متصل شده اند و به آن اجازه می دهند اطلاعات را ذخیره کند. آموزش فقط در مرحله بازخوانی انجام می شود، زیرا دینامیک مخزن ثابت است، و این چارچوب امکان استفاده از سیستم های طبیعی در دسترس، هم کلاسیک و هم مکانیک کوانتومی را برای کاهش هزینه محاسباتی موثر فراهم می کند. یکی از مزایای کلیدی محاسبات مخزن این است که امکان یک الگوریتم یادگیری ساده و سریع و همچنین اجرای سخت افزار از طریق مخازن فیزیکی را فراهم می کند . [13] [14]

محاسبات ملموس [ ویرایش ]

مقالات اصلی: رابط کاربری Claytronics و Tangible

SandScape ، یک دستگاه محاسباتی ملموس نصب شده در موزه خلاقیت کودکان در سانفرانسیسکو

محاسبات ملموس به استفاده از اشیاء فیزیکی به عنوان رابط کاربری برای تعامل با اطلاعات دیجیتال اشاره دارد. هدف این رویکرد بهره گیری از توانایی انسان برای درک و دستکاری اشیاء فیزیکی به منظور تسهیل همکاری، یادگیری و طراحی است. ویژگی‌های رابط‌های کاربری ملموس شامل جفت کردن نمایش‌های فیزیکی با اطلاعات دیجیتالی زیربنایی و تجسم مکانیسم‌هایی برای کنترل تعاملی است. [15] همچنین پنج ویژگی تعیین کننده رابط کاربری ملموس وجود دارد، از جمله توانایی چندگانه سازی ورودی و خروجی در فضا، دسترسی همزمان و دستکاری اجزای رابط، دستگاه های خاص قوی، دستگاه های محاسباتی آگاه از فضای مکانی، و پیکربندی مجدد مکانی دستگاه ها. [16]

محاسبات انسانی [ ویرایش ]

مقاله اصلی: کامپیوتر انسان

اصطلاح "کامپیوتر انسانی" به افرادی اطلاق می‌شود که محاسبات ریاضی را به صورت دستی انجام می‌دهند و اغلب به صورت گروهی کار می‌کنند و از قوانین ثابت پیروی می‌کنند. در گذشته برای انجام محاسبات طولانی و طاقت فرسا، تیم هایی متشکل از افراد، اغلب زنان، به کار گرفته می شدند و کار به صورت موازی انجام می شد. این اصطلاح اخیراً برای توصیف افرادی با مهارت‌های حسابی ذهنی استثنایی که به عنوان ماشین‌حساب ذهنی نیز شناخته می‌شوند، استفاده می‌شود. [17]

تعامل انسان و ربات [ ویرایش ]

مقالات اصلی: تعامل انسان و ربات و Cobot

تعامل انسان و ربات

تعامل انسان و ربات ، یا HRI، مطالعه تعامل بین انسان و روبات است. این شامل مشارکت در زمینه هایی مانند هوش مصنوعی، رباتیک و روانشناسی است. ربات‌ها یا روبات‌های مشارکتی برای تعامل مستقیم با انسان‌ها در فضاهای مشترک طراحی شده‌اند و می‌توانند برای انواع وظایف، [18] از جمله ارائه اطلاعات، لجستیک و وظایف غیر ارگونومیک در محیط‌های صنعتی استفاده شوند.

محاسبات ازدحام [ ویرایش ]

مقالات اصلی: رباتیک ازدحام و هوش ازدحامی

رباتیک ازدحام یک رشته مطالعاتی است که بر هماهنگی و کنترل ربات های متعدد به عنوان یک سیستم متمرکز است. رباتیک ازدحام با الهام از رفتار نوظهور مشاهده شده در حشرات اجتماعی شامل استفاده از قوانین فردی نسبتا ساده برای ایجاد رفتارهای گروهی پیچیده از طریق ارتباط محلی و تعامل با محیط است. [19] این رویکرد با استفاده از تعداد زیادی ربات ساده مشخص می‌شود و مقیاس‌پذیری را از طریق استفاده از روش‌های ارتباطی محلی مانند فرکانس رادیویی یا مادون قرمز ارتقا می‌دهد.

رویکردهای فیزیک [ ویرایش ]

محاسبات نوری [ ویرایش ]

مقاله اصلی: محاسبات نوری

تحقق یک گیت کنترل‌شده فوتونیکی برای استفاده در محاسبات کوانتومی

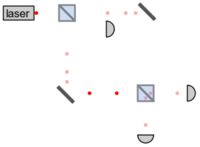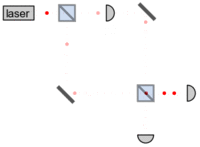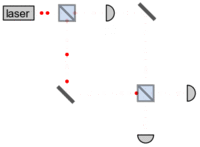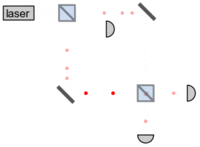
محاسبات نوری نوعی محاسبات است که از امواج نور که اغلب توسط لیزر یا منابع نامنسجم تولید می‌شوند، برای پردازش، ذخیره‌سازی و ارتباطات استفاده می‌کند. در حالی که این فناوری پتانسیل ارائه پهنای باند بالاتری نسبت به رایانه‌های سنتی که از الکترون‌ها استفاده می‌کنند را دارد، دستگاه‌های الکترونیک نوری می‌توانند مقدار قابل توجهی انرژی را در فرآیند تبدیل انرژی الکترونیکی به فوتون و برگشت مصرف کنند. هدف کامپیوترهای تمام نوری حذف نیاز به این تبدیل ها است که منجر به کاهش مصرف برق می شود. [20] کاربردهای محاسبات نوری شامل رادار با دیافراگم مصنوعی و همبسته‌های نوری است که می‌توانند برای تشخیص، ردیابی و طبقه‌بندی شی مورد استفاده قرار گیرند. [21] [22]

اسپینترونیکس [ ویرایش ]

مقاله اصلی: اسپینترونیکس

اسپینترونیک رشته‌ای است که شامل استفاده از اسپین ذاتی و گشتاور مغناطیسی الکترون‌ها در دستگاه‌های حالت جامد است. [23] [24] [25] تفاوت آن با الکترونیک سنتی در این است که از اسپین الکترون ها به عنوان یک درجه آزادی اضافی استفاده می کند که کاربردهای بالقوه ای در ذخیره سازی و انتقال داده ها، [26] و همچنین محاسبات کوانتومی و نورومورفیک دارد. سیستم های اسپینترونیک اغلب با استفاده از نیمه هادی های مغناطیسی رقیق و آلیاژهای هوسلر ایجاد می شوند.

اتمترونیک [ ویرایش ]

مقاله اصلی: Atomtronics

Atomtronics شکلی از محاسبات است که شامل استفاده از اتم های فوق سرد در مدارهای موج ماده منسجم است که می تواند دارای اجزایی شبیه به آنچه در سیستم های الکترونیکی یا نوری یافت می شود. [27] [28] این مدارها کاربردهای بالقوه ای در چندین زمینه دارند، از جمله تحقیقات فیزیک بنیادی و توسعه ابزارهای عملی مانند حسگرها و کامپیوترهای کوانتومی.

سیالات [ ویرایش ]

مقاله اصلی: سیالات

فلیپ فلاپ ساخته شده با استفاده از مایعات.

سیالات یا منطق سیالات، استفاده از دینامیک سیالات برای انجام عملیات آنالوگ یا دیجیتال در محیط‌هایی است که الکترونیک ممکن است غیرقابل اعتماد باشد، مانند محیط‌هایی که در معرض سطوح بالای تداخل الکترومغناطیسی یا تشعشعات یونیزان هستند. دستگاه های سیال بدون قطعات متحرک کار می کنند و می توانند از تقویت غیر خطی مشابه ترانزیستورها در منطق دیجیتال الکترونیکی استفاده کنند. سیالات در نانوتکنولوژی و کاربردهای نظامی نیز کاربرد دارند.

محاسبات کوانتومی [ ویرایش ]

مقاله اصلی: محاسبات کوانتومی

محاسبات کوانتومی، شاید شناخته‌شده‌ترین و توسعه‌یافته‌ترین روش محاسباتی غیر متعارف، نوعی از محاسبات است که از اصول مکانیک کوانتومی مانند برهم‌نهی و درهم‌تنیدگی برای انجام محاسبات استفاده می‌کند. [29] [30] رایانه‌های کوانتومی از کیوبیت‌هایی استفاده می‌کنند که مشابه بیت‌های کلاسیک هستند اما می‌توانند در چندین حالت به طور همزمان وجود داشته باشند تا عملیات را انجام دهند. در حالی که رایانه‌های کوانتومی کنونی ممکن است هنوز در کاربردهای عملی از رایانه‌های کلاسیک بهتر عمل نکنند، آنها پتانسیل حل مشکلات محاسباتی خاصی مانند فاکتورسازی اعداد صحیح را دارند که به طور قابل توجهی سریع‌تر از رایانه‌های کلاسیک هستند. با این حال، چندین چالش برای ساخت رایانه‌های کوانتومی عملی وجود دارد، از جمله دشواری حفظ حالت‌های کوانتومی کیوبیت‌ها و نیاز به تصحیح خطا. [31] [32] نظریه پیچیدگی کوانتومی مطالعه پیچیدگی محاسباتی مسائل با توجه به کامپیوترهای کوانتومی است.

یک کامپیوتر کوانتومی

محاسبات ابررسانا [ ویرایش ]

مقاله اصلی: محاسبات ابررسانا

محاسبات ابررسانا شکلی از محاسبات برودتی است که از ویژگی‌های منحصر به فرد ابررساناها، از جمله سیم‌های مقاومت صفر و سوئیچینگ فوق سریع، برای رمزگذاری، پردازش و انتقال داده‌ها با استفاده از کوانتوم‌های شار واحد استفاده می‌کند. اغلب در محاسبات کوانتومی استفاده می شود و برای عملیات نیاز به خنک سازی تا دمای برودتی دارد.

سیستم های میکروالکترومکانیکی [ ویرایش ]

مقاله‌های اصلی: سیستم‌های میکروالکترومکانیکی و سیستم‌های نانوالکترومکانیکی

سیستم‌های میکروالکترومکانیکی (MEMS) و سیستم‌های نانو الکترومکانیکی (NEMS) فناوری‌هایی هستند که شامل استفاده از دستگاه‌های میکروسکوپی با قطعات متحرک، از میکرومتر تا نانومتر می‌شوند. این دستگاه‌ها معمولاً از یک واحد پردازش مرکزی (مانند یک مدار مجتمع) و چندین مؤلفه که با محیط اطراف خود تعامل دارند، مانند حسگرها، تشکیل شده‌اند. [33] فن آوری MEMS و NEMS با نانوتکنولوژی مولکولی یا الکترونیک مولکولی متفاوت است زیرا آنها عواملی مانند شیمی سطح و اثرات الکترومغناطیس محیط و دینامیک سیالات را نیز در نظر می گیرند. از کاربردهای این فناوری ها می توان به شتاب سنج ها و حسگرهای تشخیص مواد شیمیایی اشاره کرد. [34]

رویکردهای شیمی [ ویرایش ]

نمایش گرافیکی یک روتاکسان ، مفید به عنوان یک سوئیچ مولکولی

محاسبات مولکولی [ ویرایش ]

مقالات اصلی: الکترونیک مقیاس مولکولی ، محاسبات شیمیایی ، و دروازه منطق مولکولی

محاسبات مولکولی شکلی غیر متعارف از محاسبات است که از واکنش های شیمیایی برای انجام محاسبات استفاده می کند. داده ها با تغییرات در غلظت های شیمیایی نشان داده می شوند، [35] و هدف این نوع محاسبات استفاده از کوچک ترین ساختارهای پایدار، مانند مولکول های منفرد، به عنوان اجزای الکترونیکی است. این میدان که به عنوان محاسبات شیمیایی یا محاسبات واکنش انتشار نیز شناخته می‌شود، از زمینه‌های مرتبط پلیمرهای رسانا و الکترونیک آلی که از مولکول‌ها برای تأثیرگذاری بر خواص توده‌ای مواد استفاده می‌کنند، متمایز است.

رویکردهای بیوشیمی [ ویرایش ]

محاسبات پپتید [ ویرایش ]

مقاله اصلی: محاسبات پپتید

محاسبات پپتید یک مدل محاسباتی است که از پپتیدها و آنتی بادی ها برای حل مسائل NP-complete استفاده می کند و نشان داده شده است که از نظر محاسباتی جهانی است. مزایایی نسبت به محاسبات DNA مانند تعداد بیشتر بلوک‌های ساختمانی و برهمکنش‌های انعطاف‌پذیرتر دارد، اما به دلیل در دسترس بودن محدود آنتی‌بادی‌های مونوکلونال خاص، هنوز عملاً محقق نشده است. [36] [37]

محاسبات DNA [ ویرایش ]

مقاله اصلی: محاسبات DNA

محاسبات DNA شاخه ای از محاسبات غیر متعارف است که از DNA و سخت افزار زیست شناسی مولکولی برای انجام محاسبات استفاده می کند. این نوعی از محاسبات موازی است که می تواند برخی از مسائل تخصصی را سریعتر و کارآمدتر از رایانه های الکترونیکی سنتی حل کند. در حالی که محاسبات DNA هیچ قابلیت جدیدی از نظر تئوری محاسباتی ارائه نمی دهد، می تواند تعداد زیادی محاسبات موازی را به طور همزمان انجام دهد. با این حال، محاسبات DNA سرعت پردازش کمتری دارد و تجزیه و تحلیل نتایج در مقایسه با کامپیوترهای دیجیتال دشوارتر است.

محاسبات غشایی [ ویرایش ]

مقاله اصلی: محاسبات غشایی

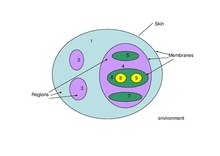
کامپیوتر غشایی Nine Region

محاسبات غشایی، همچنین به عنوان سیستم های P شناخته می شود، [38] زیر شاخه ای از علوم کامپیوتر است که مدل های محاسباتی توزیع شده و موازی را بر اساس ساختار و عملکرد غشاهای بیولوژیکی مطالعه می کند. در این سیستم‌ها، اشیایی مانند نمادها یا رشته‌ها در محفظه‌هایی که توسط غشاها تعریف شده‌اند پردازش می‌شوند و ارتباط بین محفظه‌ها و با محیط خارجی نقش مهمی در محاسبات بازی می‌کند. سیستم های P سلسله مراتبی هستند و می توانند به صورت گرافیکی نمایش داده شوند، با قوانینی که بر تولید، مصرف و حرکت اشیاء در داخل و بین مناطق حاکم است. در حالی که این سیستم‌ها تا حد زیادی تئوری باقی مانده‌اند، [39] برخی از آنها پتانسیل حل مسائل NP-complete را دارند و به عنوان پیاده‌سازی سخت‌افزاری برای محاسبات غیر متعارف پیشنهاد شده‌اند.

رویکردهای بیولوژیکی [ ویرایش ]

مقالات اصلی: محاسبات با الهام از بیولوژیکی ، محاسبات طبیعی ، و محاسبات بیولوژیکی

محاسبات بیولوژیکی که به عنوان محاسبات الهام گرفته از زیست یا محاسبات طبیعی نیز شناخته می شود، مطالعه استفاده از مدل های الهام گرفته از زیست شناسی برای حل مسائل علوم کامپیوتر، به ویژه در زمینه های هوش مصنوعی و یادگیری ماشین است. این شامل طیف وسیعی از پارادایم‌های محاسباتی از جمله شبکه‌های عصبی مصنوعی، الگوریتم‌های تکاملی، هوش ازدحام، سیستم‌های ایمنی مصنوعی و موارد دیگر است که می‌توانند با استفاده از سخت‌افزار الکترونیکی سنتی یا رسانه‌های فیزیکی جایگزین مانند بیومولکول‌ها یا دستگاه‌های محاسباتی کوانتومی یون به دام افتاده پیاده‌سازی شوند. همچنین شامل مطالعه درک سیستم های بیولوژیکی از طریق مهندسی ارگانیسم های نیمه مصنوعی و مشاهده فرآیندهای طبیعی به عنوان پردازش اطلاعات است. مفهوم خود جهان به عنوان یک مکانیسم محاسباتی نیز پیشنهاد شده است. [40] [41]

علوم اعصاب [ ویرایش ]

مقاله‌های اصلی: محاسبات نورومورفیک و رایانه مرطوب‌افزار

محاسبات نورومورفیک شامل استفاده از مدارهای الکترونیکی برای تقلید از معماری‌های عصبی زیست‌شناختی موجود در سیستم عصبی انسان، با هدف ایجاد سیستم‌های عصبی مصنوعی است که از سیستم‌های بیولوژیکی الهام گرفته شده‌اند. [42] [43] این سیستم ها را می توان با استفاده از انواع سخت افزارها، مانند ممریستورها، [44] حافظه های اسپینترونیک، و ترانزیستورها، [45] [46] پیاده سازی کرد و می توان با استفاده از طیف وسیعی از رویکردهای مبتنی بر نرم افزار، از جمله آموزش داد. پس انتشار خطا [47] و قوانین یادگیری متعارف. [48] رشته مهندسی نورومورفیک به دنبال درک چگونگی تأثیر طراحی و ساختار سیستم‌های عصبی مصنوعی بر محاسبات، نمایش اطلاعات، سازگاری و عملکرد کلی است، با هدف نهایی ایجاد سیستم‌هایی که ویژگی‌های مشابه با آنچه در طبیعت وجود دارد را نشان می‌دهند. . کامپیوترهای مرطوب‌افزار که از نورون‌های زنده تشکیل شده‌اند، شکلی مفهومی از محاسبات نورومورفیک هستند که در نمونه‌های اولیه محدودی مورد بررسی قرار گرفته‌اند. [49]

اتوماتای سلولی و محاسبات آمورف [ ویرایش ]

مقالات اصلی: اتوماتای سلولی و محاسبات آمورف

اسلحه گلایدر Gosper در بازی زندگی کانوی اتومات سلولی " گلایدر " ایجاد می کند [50]

اتوماتای سلولی مدل‌های مجزای محاسباتی هستند که از شبکه‌ای از سلول‌ها در تعداد محدودی حالت‌ها مانند روشن و خاموش تشکیل شده‌اند. وضعیت هر سلول توسط یک قانون ثابت بر اساس حالات سلول و همسایگان آن تعیین می شود. چهار طبقه‌بندی اولیه از اتوماتای سلولی وجود دارد، از الگوهایی که به یکنواختی تثبیت می‌شوند تا آنهایی که بسیار پیچیده و بالقوه تورینگ کامل می‌شوند. محاسبات آمورف به مطالعه سیستم‌های محاسباتی با استفاده از تعداد زیادی پردازنده‌های موازی با توانایی محاسباتی محدود و تعاملات محلی، بدون توجه به بستر فیزیکی اشاره دارد. نمونه هایی از محاسبات آمورف طبیعی را می توان در زیست شناسی رشد، زیست شناسی مولکولی، شبکه های عصبی و مهندسی شیمی یافت. هدف محاسبات آمورف درک و مهندسی سیستم های جدید از طریق توصیف الگوریتم های آمورف به عنوان انتزاع است.

محاسبات تکاملی [ ویرایش ]

مقاله اصلی: محاسبات تکاملی

محاسبات تکاملی نوعی هوش مصنوعی و محاسبات نرم است که از الگوریتم های الهام گرفته از تکامل بیولوژیکی برای یافتن راه حل های بهینه برای طیف وسیعی از مسائل استفاده می کند. این شامل تولید یک مجموعه اولیه از راه حل های نامزد، حذف تصادفی راه حل های کمتر مورد نظر، و ایجاد تغییرات تصادفی کوچک برای ایجاد یک نسل جدید است. جمعیت محلول‌ها در معرض انتخاب و جهش طبیعی یا مصنوعی قرار می‌گیرند که منجر به تکامل به سمت افزایش تناسب با توجه به تابع تناسب اندام انتخابی می‌شود. محاسبات تکاملی در تنظیمات مختلف مشکل مؤثر بوده و در علوم کامپیوتر و زیست‌شناسی تکاملی کاربرد دارد.

رویکردهای ریاضی [ ویرایش ]

محاسبات سه تایی [ ویرایش ]

مقاله اصلی: محاسبات سه تایی

محاسبات سه تایی نوعی از محاسبات است که از منطق سه تایی یا پایه 3 در محاسبات خود به جای سیستم باینری رایج تر استفاده می کند . کامپیوترهای سه تایی از تریت ها یا ارقام سه تایی استفاده می کنند که می توانند به روش های مختلفی تعریف شوند، از جمله منطق سه تایی نامتعادل، سه تایی نامتعادل کسری، سه تایی متعادل و منطق حالت مجهول. کامپیوترهای کوانتومی سه تایی به جای تریت از کوتریت استفاده می کنند. محاسبات سه تایی تا حد زیادی با رایانه های دوتایی جایگزین شده است، اما برای استفاده در دستگاه های پرسرعت و کم مصرف با استفاده از اتصال جوزفسون به عنوان یک سلول حافظه سه تایی متعادل پیشنهاد شده است.

محاسبات برگشت پذیر [ ویرایش ]

مقاله اصلی: محاسبات برگشت پذیر

محاسبات برگشت پذیر نوعی از محاسبات غیر متعارف است که در آن فرآیند محاسباتی می تواند تا حدی معکوس شود. برای اینکه یک محاسبه برگشت پذیر باشد، رابطه بین حالت ها و جانشینان آنها باید یک به یک باشد و این فرآیند نباید منجر به افزایش آنتروپی فیزیکی شود. مدارهای کوانتومی تا زمانی که حالت های کوانتومی را جمع نکنند برگشت پذیر هستند و توابع برگشت پذیر دوجکتیو هستند، به این معنی که تعداد ورودی های آنها برابر با خروجی ها است. [51]

محاسبات آشوب [ ویرایش ]

مقاله اصلی: محاسبات آشوب

محاسبات آشوب گونه ای از محاسبات غیر متعارف است که از سیستم های آشفته برای انجام محاسبات استفاده می کند. سیستم های آشوبی را می توان برای ایجاد دروازه های منطقی مورد استفاده قرار داد و می تواند به سرعت بین الگوهای مختلف جابجا شود و آنها را برای برنامه های کاربردی مقاوم به خطا و محاسبات موازی مفید می کند. محاسبات آشوب در زمینه های مختلفی مانند هواشناسی، فیزیولوژی و مالی استفاده شده است.

محاسبات تصادفی [ ویرایش ]

مقاله اصلی: محاسبات تصادفی

محاسبات تصادفی یک روش محاسباتی است که مقادیر پیوسته را به صورت جریانی از بیت های تصادفی نشان می دهد و عملیات پیچیده را با استفاده از عملیات بیتی ساده بر روی جریان ها انجام می دهد. می توان آن را به عنوان یک کامپیوتر ترکیبی آنالوگ/دیجیتال مشاهده کرد و با خاصیت دقت پیشرونده آن مشخص می شود، جایی که دقت محاسبات با گسترش جریان بیت افزایش می یابد. محاسبات تصادفی می تواند در سیستم های تکرار شونده برای دستیابی به همگرایی سریعتر مورد استفاده قرار گیرد، اما همچنین می تواند به دلیل نیاز به تولید جریان بیت تصادفی پرهزینه باشد و در صورت عدم رعایت فرض جریان های بیت مستقل، در برابر شکست آسیب پذیر است. همچنین توانایی آن برای انجام برخی عملکردهای دیجیتال محدود است.

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Unconventional_computing

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:9 توسط علی رضا نقش |

5-محاسبات کوانتومی

نامزدهای تحقق فیزیکی [ ویرایش ]

اطلاعات بیشتر: فهرست رجیسترهای کوانتومی پیشنهادی

این بخش نیاز به گسترش دارد . می توانید با افزودن به آن کمک کنید . ( ژوئیه 2023 )

یک کامپیوتر کوانتومی عملی باید از یک سیستم فیزیکی به عنوان یک ثبات کوانتومی قابل برنامه ریزی استفاده کند. [140] محققان در حال بررسی چندین فناوری به عنوان کاندیدای اجرای کیوبیت قابل اعتماد هستند. [141] ابررساناها و یون‌های به دام افتاده برخی از پیشرفته‌ترین پیشنهادها هستند، اما آزمایش‌گران احتمالات سخت‌افزاری دیگری را نیز در نظر می‌گیرند. [142]

تئوری[ ویرایش ]

محاسبه پذیری[ ویرایش ]

اطلاعات بیشتر: نظریه محاسباتی

هر مشکل محاسباتی قابل حل توسط یک کامپیوتر کلاسیک توسط یک کامپیوتر کوانتومی نیز قابل حل است. [143] به طور شهودی، این به این دلیل است که اعتقاد بر این است که همه پدیده‌های فیزیکی، از جمله عملکرد رایانه‌های کلاسیک، می‌توانند با استفاده از مکانیک کوانتومی ، که زیربنای عملکرد رایانه‌های کوانتومی است، توصیف شوند.

برعکس، هر مشکلی که توسط یک کامپیوتر کوانتومی قابل حل باشد، توسط یک کامپیوتر کلاسیک نیز قابل حل است. اگر زمان کافی داده شود، می توان کامپیوترهای کوانتومی و کلاسیک را به صورت دستی فقط با مقداری کاغذ و قلم شبیه سازی کرد. به طور رسمی تر، هر کامپیوتر کوانتومی را می توان توسط ماشین تورینگ شبیه سازی کرد . به عبارت دیگر، رایانه‌های کوانتومی از نظر قابلیت محاسبه ، هیچ قدرت اضافی نسبت به رایانه‌های کلاسیک ارائه نمی‌کنند . این بدان معناست که رایانه‌های کوانتومی نمی‌توانند مسائل غیرقابل تصمیم‌گیری مانند مشکل توقف را حل کنند ، و وجود رایانه‌های کوانتومی تز چرچ-تورینگ را رد نمی‌کند . [144]

پیچیدگی[ ویرایش ]

مقاله اصلی: نظریه پیچیدگی کوانتومی

در حالی که رایانه‌های کوانتومی نمی‌توانند مشکلاتی را که رایانه‌های کلاسیک قبلاً نمی‌توانند حل کنند، حل کنند، گمان می‌رود که آنها می‌توانند مشکلات خاصی را سریع‌تر از رایانه‌های کلاسیک حل کنند. به عنوان مثال، مشخص است که رایانه‌های کوانتومی می‌توانند به طور مؤثر اعداد صحیح را فاکتور بگیرند ، در حالی که تصور نمی‌شود این مورد برای رایانه‌های کلاسیک باشد.

دسته ای از مسائلی که می توانند به طور موثر توسط یک کامپیوتر کوانتومی با خطای محدود حل شوند ، BQP برای "خطای محدود، کوانتومی، زمان چند جمله ای" نامیده می شود. به طور رسمی تر، BQP کلاس مسائلی است که می تواند توسط یک ماشین تورینگ کوانتومی چند جمله ای با احتمال خطا حداکثر 1/3 حل شود. به عنوان یک کلاس از مسائل احتمالی، BQP همتای کوانتومی BPP است ("خطای محدود، احتمالی، زمان چند جمله ای")، کلاسی از مسائلی که می توانند توسط ماشین های تورینگ احتمالی چند جمله ای با خطای کران حل شوند. [145] معروف است کهبپپ⊆بسپ ${\mathsf {BPP\subseteq BQP}}$ و به طور گسترده مشکوک است کهبسپ⊊بپپ ${\mathsf {BQP\subsetneq BPP}}$ ، که به طور شهودی به این معنی است که رایانه های کوانتومی از نظر پیچیدگی زمانی قوی تر از رایانه های کلاسیک هستند . [146]

رابطه مشکوک BQP با چندین کلاس پیچیدگی کلاسیک [64]

رابطه دقیق BQP با P ، NP و PSPACE مشخص نیست. با این حال، مشخص است کهپ⊆بسپ⊆پاسپآسی� ${\mathsf {P\subseteq BQP\subseteq PSPACE}}$ ; یعنی تمام مسائلی را که می توان به طور کارآمد با یک کامپیوتر کلاسیک قطعی حل کرد، توسط یک کامپیوتر کوانتومی نیز می تواند به طور کارآمد حل شود، و تمام مسائلی که می توانند به طور موثر توسط یک کامپیوتر کوانتومی حل شوند نیز می توانند توسط یک کامپیوتر کلاسیک قطعی با منابع فضایی چند جمله ای حل شوند. . همچنین گمان می رود که BQP یک ابرمجموعه سخت P است، به این معنی که مشکلاتی وجود دارد که به طور مؤثر توسط رایانه های کوانتومی قابل حل هستند که به طور کارآمدی توسط رایانه های کلاسیک قطعی قابل حل نیستند. برای مثال، فاکتورسازی اعداد صحیح و مسئله لگاریتم گسسته در BQP شناخته شده است و مشکوک به خارج از P است. P نیز در BQP هستند (مثلاً فاکتورسازی عدد صحیح و مسئله لگاریتم گسسته هر دو در NP هستند). مشکوک است کهنپ⊈بسپ ${\mathsf {NP\nsubseteq BQP}}$ ; یعنی اعتقاد بر این است که مسائلی وجود دارد که به طور موثر قابل بررسی هستند که به طور کارآمدی توسط یک کامپیوتر کوانتومی قابل حل نیستند. به عنوان پیامد مستقیم این باور، همچنین گمان می رود که BQP از کلاس مسائل NP-complete جدا باشد (اگر یک مسئله NP-کامل در BQP باشد، پس از سختی NP نتیجه می گیرد که همه مشکلات در NP در BQP). [147]

همچنین ببینید [ ویرایش ]

D-Wave Systems - شرکت کانادایی محاسبات کوانتومی
هولوگرافی کوانتومی الکترونیکی
واژه نامه محاسبات کوانتومی
IARPA - آژانس دولتی آمریکا
فهرست فناوری‌های نوظهور – فناوری‌های جدید فعالانه در حال توسعه هستند
فهرست پردازنده های کوانتومی – فهرست اجزای کامپیوتر کوانتومی
تقطیر حالت جادویی - الگوریتم محاسبات کوانتومی
محاسبات طبیعی - اصطلاحات معرفی شده برای شامل سه دسته از روش ها
محاسبات نوری - رایانه ای که از فوتون ها یا امواج نور استفاده می کند
گذرگاه کوانتومی - دستگاهی که می تواند برای ذخیره یا انتقال اطلاعات بین کیوبیت های مستقل در یک کامپیوتر کوانتومی استفاده شود
شناخت کوانتومی - کاربرد مکانیک کوانتومی در پدیده های شناختی
حجم کوانتومی – متریک برای قابلیت های یک کامپیوتر کوانتومی
عجیب بودن کوانتومی - جنبه های غیر شهودی مکانیک کوانتومی
Rigetti Computing - شرکت محاسبات کوانتومی آمریکایی
ابررایانه - نوعی کامپیوتر بسیار قدرتمند
علوم کامپیوتر نظری - زیر شاخه علوم کامپیوتر و ریاضیات
محاسبات غیر متعارف - محاسبات با روش های جدید یا غیر معمول
Valleytronics - منطقه آزمایشی در نیمه هادی ها

https://en.wikipedia.org/wiki/Quantum_computing

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:5 توسط علی رضا نقش |

4-محاسبات کوانتومی

مهندسی[ ویرایش ]

ویفری از کامپیوترهای کوانتومی آدیاباتیک

از سال 2023، رایانه های کلاسیک برای همه برنامه های کاربردی دنیای واقعی از رایانه های کوانتومی بهتر عمل می کنند. در حالی که کامپیوترهای کوانتومی فعلی ممکن است راه حل های مسائل ریاضی خاص را سرعت بخشند، اما هیچ مزیت محاسباتی برای کارهای عملی ندارند. برای بسیاری از کارها هیچ وعده افزایش سرعت کوانتومی مفیدی وجود ندارد، و برخی از کارها به طور قابل اثباتی هرگونه افزایش سرعت کوانتومی را ممنوع می کنند به این معنا که هر گونه افزایش سرعت توسط قضایای اثبات شده رد می شود. دانشمندان و مهندسان در حال بررسی فناوری‌های متعدد برای سخت‌افزار محاسبات کوانتومی هستند و امیدوارند که معماری‌های کوانتومی مقیاس‌پذیر را توسعه دهند، اما موانع جدی همچنان وجود دارد. [94] [95]

چالش ها [ ویرایش ]

تعدادی از چالش های فنی در ساخت یک کامپیوتر کوانتومی در مقیاس بزرگ وجود دارد. [96] فیزیکدان دیوید دی وینچنزو این الزامات را برای یک کامپیوتر کوانتومی عملی فهرست کرده است : [97]

از نظر فیزیکی مقیاس پذیر برای افزایش تعداد کیوبیت ها
کیوبیت هایی که می توانند به مقادیر دلخواه مقداردهی اولیه شوند
دروازه‌های کوانتومی که سریع‌تر از زمان ناهمدوسی هستند
ست دروازه جهانی
کیوبیت هایی که به راحتی قابل خواندن هستند.

تامین قطعات برای کامپیوترهای کوانتومی نیز بسیار دشوار است. کامپیوترهای کوانتومی ابررسانا ، مانند آنهایی که توسط گوگل و IBM ساخته شده اند، به هلیوم-3 ، محصول جانبی تحقیقات هسته ای و کابل های ابررسانای ویژه ای نیاز دارند که فقط توسط شرکت ژاپنی کواکس ساخته شده است. [98]

کنترل سیستم های چند کیوبیتی مستلزم تولید و هماهنگی تعداد زیادی سیگنال الکتریکی با وضوح زمان بندی دقیق و قطعی است. این منجر به توسعه کنترل‌کننده‌های کوانتومی شده است که ارتباط با کیوبیت‌ها را امکان‌پذیر می‌کنند. مقیاس بندی این سیستم ها برای پشتیبانی از تعداد فزاینده کیوبیت ها یک چالش اضافی است. [99]

عدم انسجام[ ویرایش ]

یکی از بزرگترین چالش‌های موجود در ساخت رایانه‌های کوانتومی، کنترل یا حذف ناهمدوسی کوانتومی است . این معمولاً به معنای جداسازی سیستم از محیط خود است زیرا تعاملات با دنیای بیرونی باعث جدا شدن سیستم می شود. با این حال، منابع دیگری از عدم انسجام نیز وجود دارد. به عنوان مثال می توان به دروازه های کوانتومی و ارتعاشات شبکه و اسپین گرما هسته ای پس زمینه سیستم فیزیکی که برای اجرای کیوبیت ها استفاده می شود اشاره کرد. عدم انسجام برگشت ناپذیر است، زیرا عملاً غیر واحد است و معمولاً چیزی است که اگر از آن اجتناب نشود، باید به شدت کنترل شود. زمان‌های ناهمدوسی به‌ویژه برای سیستم‌های کاندید، زمان آرامش عرضی T2 (برای فناوری NMR و MRI ، که زمان کاهش فاز نیز نامیده می‌شود )، معمولاً بین نانوثانیه و ثانیه در دمای پایین متغیر است. [100] در حال حاضر، برخی از کامپیوترهای کوانتومی به منظور جلوگیری از انسجام قابل توجه، به کیوبیت‌هایشان نیاز دارند که تا 20 میلی‌کلوین (معمولاً از یک یخچال رقیق‌سازی استفاده می‌کنند ) خنک شوند. [102] مطالعه‌ای در سال 2020 استدلال می‌کند که پرتوهای یونیزان مانند پرتوهای کیهانی می‌توانند باعث شوند که سیستم‌های خاصی در عرض میلی‌ثانیه جدا شوند. [103]

در نتیجه، کارهای وقت‌گیر ممکن است برخی از الگوریتم‌های کوانتومی را غیرقابل اجرا کند، زیرا تلاش برای حفظ وضعیت کیوبیت‌ها برای مدت زمان کافی طولانی، در نهایت برهم‌نهی‌ها را خراب می‌کند. [104]

این مسائل برای رویکردهای نوری دشوارتر هستند، زیرا مقیاس‌های زمانی مرتبه‌ای کوتاه‌تر هستند و یک رویکرد غالباً برای غلبه بر آنها شکل‌دهی پالس نوری است . نرخ خطا معمولاً متناسب با نسبت زمان عملیاتی به زمان ناپیوستگی است، از این رو هر عملیاتی باید بسیار سریعتر از زمان ناپیوستگی کامل شود.

همانطور که توسط قضیه آستانه توضیح داده شد ، اگر میزان خطا به اندازه کافی کوچک باشد، تصور می‌شود که می‌توان از تصحیح خطای کوانتومی برای سرکوب خطاها و ناپیوستگی استفاده کرد. در صورتی که طرح تصحیح خطا بتواند خطاها را سریعتر از زمانی که decoherence معرفی می کند، تصحیح کند، این اجازه می دهد تا کل زمان محاسبه بیشتر از زمان عدم انسجام باشد. رقمی که اغلب برای نرخ خطای مورد نیاز در هر گیت برای محاسبات تحمل‌پذیر خطا ذکر می‌شود، 10-3 است ، با این فرض که نویز دپلاریزاسیون است.

تحقق این شرط مقیاس پذیری برای طیف وسیعی از سیستم ها امکان پذیر است. با این حال، استفاده از تصحیح خطا هزینه افزایش بسیار زیادی از کیوبیت های مورد نیاز را به همراه دارد. عدد مورد نیاز برای فاکتورسازی اعداد صحیح با استفاده از الگوریتم Shor هنوز چند جمله‌ای است و گمان می‌رود بین L و L 2 باشد . الگوریتم های تصحیح خطا این رقم را با ضریب L افزایش می دهد . برای یک عدد 1000 بیتی، این به معنای نیاز به حدود 10 4 بیت بدون تصحیح خطا است. [105] با تصحیح خطا، این رقم به حدود 10 7 بیت افزایش می یابد. زمان محاسبه حدود L 2 یا حدود 107 گام و در 1 مگاهرتز، حدود 10 ثانیه است. با این حال، سربار رمزگذاری و تصحیح خطا، اندازه یک کامپیوتر کوانتومی متحمل خطا را با چندین مرتبه بزرگی افزایش می‌دهد. برآوردهای دقیق [106] [107] نشان می‌دهد که حداقل 3 میلیون کیوبیت فیزیکی در 5 ماه یک عدد صحیح 2048 بیتی را در یک کامپیوتر کوانتومی یونی به دام افتاده با خطای تصحیح شده کاملاً فاکتور می‌کند. از نظر تعداد کیوبیت های فیزیکی، تا به امروز، این کمترین برآورد [108] برای مسئله فاکتورسازی اعداد صحیح عملا مفید با اندازه 1024 بیتی یا بزرگتر است.

روش دیگر برای مسئله پایداری- ناهمدوسی، ایجاد یک کامپیوتر کوانتومی توپولوژیکی با آنیون‌ها ، شبه ذرات مورد استفاده به عنوان رشته‌ها، و تکیه بر نظریه braid برای تشکیل گیت‌های منطقی پایدار است. [109] [110]

برتری کوانتومی [ ویرایش ]

فیزیکدان جان پرسکیل اصطلاح برتری کوانتومی را برای توصیف شاهکار مهندسی نشان دادن این که یک دستگاه کوانتومی قابل برنامه ریزی می تواند مشکلی فراتر از توانایی های کامپیوترهای کلاسیک پیشرفته را حل کند، ابداع کرد. [111] [112] [113] مشکل لازم نیست مفید باشد، بنابراین برخی تست برتری کوانتومی را تنها به عنوان یک معیار بالقوه آینده می‌دانند. [114]

در اکتبر 2019، Google AI Quantum، با کمک ناسا، اولین کسی شد که ادعا کرد با انجام محاسبات روی رایانه کوانتومی Sycamore بیش از 3000000 برابر سریعتر از آنچه در Summit انجام می شود ، به برتری کوانتومی دست یافته است. کامپیوتر. [29] [115] [116] این ادعا متعاقباً به چالش کشیده شد: IBM بیان کرده است که Summit می‌تواند نمونه‌ها را بسیار سریع‌تر از آنچه ادعا می‌شود انجام دهد، [117] [118] و از آن زمان محققان الگوریتم‌های بهتری را برای مسئله نمونه‌گیری که برای ادعای کوانتومی استفاده می‌شود توسعه داده‌اند. برتری، کاهش قابل توجهی در شکاف بین Sycamore و ابررایانه های کلاسیک [119] [120] [121] و حتی شکست دادن آن. [122] [123] [124]

در دسامبر 2020، گروهی در USTC برای نشان دادن برتری کوانتومی ، نوعی نمونه‌برداری از بوزون را روی 76 فوتون با یک کامپیوتر کوانتومی فوتونیک به نام Jiuzhang اجرا کردند . [125] [126] [127] نویسندگان ادعا می کنند که یک ابر رایانه کلاسیک معاصر به زمان محاسباتی 600 میلیون سال نیاز دارد تا تعداد نمونه هایی را که پردازنده کوانتومی آنها می تواند در 20 ثانیه تولید کند تولید کند. [128]

ادعاهای برتری کوانتومی باعث ایجاد هیاهو در مورد محاسبات کوانتومی شده است، [129] اما آنها بر اساس وظایف محک ساخته شده ای هستند که مستقیماً کاربردهای مفید دنیای واقعی را نشان نمی دهند. [94] [130]

شک و تردید [ ویرایش ]

علیرغم امیدهای زیاد به محاسبات کوانتومی، پیشرفت قابل توجه در سخت افزار و خوش بینی در مورد برنامه های کاربردی آینده، یک مقاله نورافکن Nature در سال 2023 ، رایانه های کوانتومی فعلی را به عنوان «در حال حاضر، [برای] مطلقاً هیچ چیز [خوب]» خلاصه کرد. [94] مقاله توضیح داد که کامپیوترهای کوانتومی هنوز در هر صورت مفیدتر یا کارآمدتر از کامپیوترهای معمولی نیستند، اگرچه همچنین استدلال می‌کرد که در درازمدت چنین رایانه‌هایی احتمالاً مفید هستند. یک مقاله ACM در سال 2023 [95] نشان داد که الگوریتم‌های محاسباتی کوانتومی فعلی "برای مزیت کوانتومی عملی بدون پیشرفت‌های قابل توجه در پشته نرم‌افزار/سخت‌افزار کافی نیستند". این استدلال می‌کند که امیدوارکننده‌ترین نامزدها برای دستیابی به سرعت با رایانه‌های کوانتومی «مشکلات داده‌های کوچک» هستند، برای مثال در شیمی و علم مواد. با این حال، مقاله همچنین نتیجه می گیرد که طیف وسیعی از برنامه های کاربردی بالقوه ای که در نظر گرفته است، مانند یادگیری ماشین، "در آینده قابل پیش بینی با الگوریتم های کوانتومی فعلی به مزیت کوانتومی دست پیدا نخواهند کرد" و محدودیت های ورودی/خروجی را شناسایی کرد که افزایش سرعت را بعید می کند. "مشکلات کلان داده، سیستم های خطی بدون ساختار، و جستجوی پایگاه داده بر اساس الگوریتم گروور".

این وضعیت را می توان در چندین ملاحظات جاری و بلندمدت دنبال کرد.

سخت افزار و الگوریتم های معمولی رایانه نه تنها برای کارهای عملی بهینه شده اند، بلکه همچنان به سرعت در حال بهبود هستند، به ویژه شتاب دهنده های GPU .
سخت افزار محاسباتی کوانتومی کنونی قبل از غرق شدن در نویز، تنها مقدار محدودی درهم تنیدگی ایجاد می کند.
الگوریتم‌های کوانتومی فقط برای برخی کارها سرعت بیشتری نسبت به الگوریتم‌های معمولی ارائه می‌کنند و تطبیق این وظایف با کاربردهای عملی چالش برانگیز است. برخی از وظایف و برنامه های کاربردی امیدوارکننده به منابعی بسیار فراتر از آنچه امروز در دسترس است نیاز دارند. [131] [132] به ویژه، پردازش مقادیر زیادی از داده های غیرکوانتومی یک چالش برای کامپیوترهای کوانتومی است. [95]
برخی از الگوریتم‌های امیدوارکننده «دکوانتیزه‌شده» شده‌اند، یعنی آنالوگ‌های غیرکوانتومی آن‌ها با پیچیدگی مشابه پیدا شده‌اند.
اگر تصحیح خطای کوانتومی برای مقیاس‌سازی رایانه‌های کوانتومی به کاربردهای عملی استفاده شود، سربار آن ممکن است سرعت ارائه شده توسط بسیاری از الگوریتم‌های کوانتومی را تضعیف کند. [95]
تحلیل پیچیدگی الگوریتم‌ها گاهی اوقات مفروضات انتزاعی ایجاد می‌کند که در کاربردها صادق نیستند. برای مثال، داده‌های ورودی ممکن است از قبل به صورت کدگذاری شده در حالت‌های کوانتومی در دسترس نباشند، و «توابع اوراکل» که در الگوریتم گروور استفاده می‌شوند ، اغلب ساختار داخلی دارند که می‌توانند برای الگوریتم‌های سریع‌تر مورد سوء استفاده قرار گیرند.

به طور خاص، ساختن کامپیوترهایی با تعداد زیادی کیوبیت ممکن است بیهوده باشد، اگر آن کیوبیت ها به اندازه کافی به هم متصل نباشند و نتوانند درجه درهم تنیدگی کافی را برای مدت طولانی حفظ کنند. محققان محاسبات کوانتومی هنگام تلاش برای برتری بر رایانه‌های معمولی، اغلب به دنبال کارهای جدیدی هستند که می‌توان آنها را در رایانه‌های کوانتومی حل کرد، اما این امکان را ایجاد می‌کند که تکنیک‌های غیرکوانتومی کارآمد در پاسخ، همانطور که برای نمایش برتری کوانتومی دیده می‌شود، ایجاد شود . بنابراین، مطلوب است که مرزهای پایین‌تر در پیچیدگی بهترین الگوریتم‌های غیرکوانتومی ممکن (که ممکن است ناشناخته باشند) ثابت شود و نشان داده شود که برخی از الگوریتم‌های کوانتومی بدون علامت بر روی آن مرزها بهبود می‌یابند.

برخی از محققین نسبت به ساخت کامپیوترهای کوانتومی مقیاس پذیر ابراز تردید کرده اند، معمولاً به دلیل مسئله حفظ انسجام در مقیاس های بزرگ، اما به دلایل دیگر.

بیل اونرو در مقاله ای که در سال 1994 منتشر شد، در مورد عملی بودن رایانه های کوانتومی تردید داشت . [133] پل دیویس استدلال کرد که یک رایانه 400 کیوبیتی حتی با اطلاعات کیهانی که توسط اصل هولوگرافیک مستلزم آن است، در تضاد خواهد بود . [134] شکاکانی مانند گیل کالای تردید دارند که برتری کوانتومی هرگز حاصل شود. [135] [136] [137] فیزیکدان میخائیل دیاکونوف شک و تردید را نسبت به محاسبات کوانتومی به شرح زیر بیان کرده است:

بنابراین تعداد پارامترهای پیوسته ای که وضعیت چنین کامپیوتر کوانتومی مفیدی را در هر لحظه توصیف می کنند باید ... حدود 10 300 باشد ... آیا می توانیم یاد بگیریم که بیش از 10 300 پارامتر متغیر پیوسته را که وضعیت کوانتومی را تعریف می کنند، کنترل کنیم. چنین سیستمی؟ پاسخ من ساده است. نه، هرگز. » [138] [139]

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:2 توسط علی رضا نقش |

3-محاسبات کوانتومی

برنامه نویسی کوانتومی[ ویرایش ]

اطلاعات بیشتر: برنامه نویسی کوانتومی

تعدادی مدل از محاسبات برای محاسبات کوانتومی وجود دارد که با عناصر اساسی که محاسبات در آنها تجزیه می شود، متمایز می شوند.

آرایه دروازه[ ویرایش ]

یک نمودار مدار کوانتومی که یک دروازه تافولی را از دروازه‌های ابتدایی‌تر پیاده‌سازی می‌کند

یک آرایه دروازه کوانتومی محاسبات را به دنباله ای از دروازه های کوانتومی چند کیوبیتی تجزیه می کند . محاسبات کوانتومی را می توان به عنوان شبکه ای از گیت ها و اندازه گیری های منطق کوانتومی توصیف کرد. با این حال، هر اندازه‌گیری را می‌توان به پایان محاسبات کوانتومی موکول کرد، اگرچه این تعویق ممکن است هزینه محاسباتی داشته باشد، بنابراین بیشتر مدارهای کوانتومی شبکه‌ای را نشان می‌دهند که فقط از گیت‌های منطقی کوانتومی تشکیل شده است و هیچ اندازه‌گیری ندارد.

هر محاسبات کوانتومی (که در فرمالیسم فوق، هر ماتریس واحد اندازه است $2^{n}\times 2^{n}$ بر فراز $n$ کیوبیت ها) را می توان به عنوان شبکه ای از دروازه های منطقی کوانتومی از خانواده نسبتاً کوچکی از دروازه ها نشان داد. انتخابی از خانواده گیت که این ساختار را فعال می کند به عنوان یک مجموعه دروازه جهانی شناخته می شود ، زیرا رایانه ای که می تواند چنین مدارهایی را اجرا کند یک کامپیوتر کوانتومی جهانی است . یکی از این مجموعه های متداول شامل تمامی گیت های تک کیوبیتی و همچنین گیت CNOT از بالا می باشد. این بدان معناست که هر محاسبات کوانتومی را می توان با اجرای دنباله ای از دروازه های تک کیوبیتی همراه با گیت های CNOT انجام داد. اگرچه این مجموعه دروازه بی نهایت است، اما می توان آن را با یک مجموعه دروازه محدود با توسل به قضیه Solovay-Kitaev جایگزین کرد .

محاسبات کوانتومی مبتنی بر اندازه گیری [ ویرایش ]

یک کامپیوتر کوانتومی مبتنی بر اندازه‌گیری ، محاسبات را به دنباله‌ای از اندازه‌گیری‌های حالت بل و دروازه‌های کوانتومی تک کیوبیتی که به حالت اولیه بسیار درهم‌تنیده (یک حالت خوشه‌ای ) اعمال می‌شود، با استفاده از تکنیکی به نام تله‌پورت دروازه کوانتومی تجزیه می‌کند .

محاسبات کوانتومی آدیاباتیک [ ویرایش ]

یک کامپیوتر کوانتومی آدیاباتیک ، مبتنی بر بازپخت کوانتومی ، محاسبات را به یک تبدیل پیوسته آهسته از یک همیلتونین اولیه به یک همیلتونی نهایی، که حالت های پایه آن حاوی راه حل هستند، تجزیه می کند. [51]

محاسبات کوانتومی توپولوژیکی [ ویرایش ]

یک کامپیوتر کوانتومی توپولوژیکی محاسبات را به بافته شدن هریون در یک شبکه دوبعدی تجزیه می کند. [52]

ماشین تورینگ کوانتومی [ ویرایش ]

ماشین تورینگ کوانتومی آنالوگ کوانتومی ماشین تورینگ است . [8] همه این مدل‌های محاسبات - مدارهای کوانتومی، [53] محاسبات کوانتومی یک‌طرفه، [54] محاسبات کوانتومی آدیاباتیک، [55] و محاسبات کوانتومی توپولوژیکی [56] - نشان داده شده‌اند که معادل تورینگ کوانتومی هستند. دستگاه؛ با توجه به اجرای کامل یکی از این کامپیوترهای کوانتومی، می تواند بقیه را بدون سربار چند جمله ای بیشتر شبیه سازی کند. این معادل سازی برای رایانه های کوانتومی عملی لازم نیست، زیرا هزینه های شبیه سازی ممکن است برای عملی بودن بیش از حد بزرگ باشد.

ارتباطات [ ویرایش ]

اطلاعات بیشتر: علم اطلاعات کوانتومی

رمزنگاری کوانتومی راه های جدیدی را برای انتقال امن داده ها امکان پذیر می کند. به عنوان مثال، توزیع کلید کوانتومی از حالت های کوانتومی درهم تنیده برای ایجاد کلیدهای رمزنگاری امن استفاده می کند . [57] هنگامی که فرستنده و گیرنده حالت‌های کوانتومی را مبادله می‌کنند، می‌توانند تضمین کنند که دشمن پیام را رهگیری نمی‌کند، زیرا هر شنود غیرمجاز سیستم کوانتومی ظریف را مختل می‌کند و یک تغییر قابل تشخیص را ایجاد می‌کند. [58] با پروتکل‌های رمزنگاری مناسب ، فرستنده و گیرنده می‌توانند اطلاعات خصوصی مشترک مقاوم در برابر استراق سمع را ایجاد کنند. [13] [59]

کابل های فیبر نوری مدرن می توانند اطلاعات کوانتومی را در فواصل نسبتاً کوتاه انتقال دهند. تحقیقات تجربی در حال انجام با هدف توسعه سخت‌افزار قابل اعتمادتر (مانند تکرارکننده‌های کوانتومی)، به امید اینکه بتوان این فناوری را به شبکه‌های کوانتومی دوردست با درهم‌تنیدگی انتها به انتها مقیاس داد. از نظر تئوری، این می‌تواند کاربردهای فناوری جدید، مانند محاسبات کوانتومی توزیع‌شده و سنجش کوانتومی پیشرفته را فعال کند . [60] [61]

الگوریتم ها [ ویرایش ]

پیشرفت در یافتن الگوریتم‌های کوانتومی معمولاً بر این مدل مدار کوانتومی متمرکز است، اگرچه استثناهایی مانند الگوریتم آدیاباتیک کوانتومی وجود دارد. الگوریتم‌های کوانتومی را می‌توان تقریباً بر اساس نوع افزایش سرعتی که نسبت به الگوریتم‌های کلاسیک مربوطه به دست می‌آید، دسته‌بندی کرد. [62]

الگوریتم‌های کوانتومی که بیش از یک سرعت چندجمله‌ای را نسبت به معروف‌ترین الگوریتم کلاسیک ارائه می‌دهند، شامل الگوریتم Shor برای فاکتورگیری و الگوریتم‌های کوانتومی مرتبط برای محاسبه لگاریتم‌های گسسته ، حل معادله پل ، و به طور کلی‌تر حل مشکل گروه‌های زیرگروه پنهان برای abelian هستند . [62] این الگوریتم‌ها به مبدأ تبدیل فوریه کوانتومی بستگی دارند . هیچ دلیل ریاضی یافت نشد که نشان دهد الگوریتم کلاسیک به همان اندازه سریع نمی تواند کشف شود، اما شواهد نشان می دهد که چنین چیزی بعید است. [63] برخی از مسائل اوراکل مانند مشکل سایمون و مسئله برنشتاین-وزیرانی سرعت‌های قابل اثباتی را ارائه می‌دهند، اگرچه این در مدل پرس و جو کوانتومی است ، که یک مدل محدود است که در آن کران‌های پایین بسیار آسان‌تر برای اثبات هستند و لزوماً به افزایش سرعت ترجمه نمی‌شوند. برای مشکلات عملی

مشکلات دیگر، از جمله شبیه‌سازی فرآیندهای فیزیکی کوانتومی از شیمی و فیزیک حالت جامد، تقریب چند جمله‌ای‌های خاص جونز ، و الگوریتم کوانتومی برای سیستم‌های معادلات خطی، الگوریتم‌های کوانتومی به نظر می‌رسد که سرعت‌های فوق چند جمله‌ای را ارائه می‌دهند و BQP -کامل هستند. از آنجایی که این مشکلات BQP-کامل هستند، یک الگوریتم کلاسیک به همان اندازه سریع برای آنها نشان می‌دهد که هیچ الگوریتم کوانتومی سرعت فوق چند جمله‌ای را نمی‌دهد، که بعید به نظر می‌رسد. [64]

برخی از الگوریتم‌های کوانتومی، مانند الگوریتم گروور و تقویت دامنه ، سرعت چندجمله‌ای را نسبت به الگوریتم‌های کلاسیک مربوطه می‌دهند. [62] اگرچه این الگوریتم‌ها سرعت درجه دوم نسبتاً متوسطی را ارائه می‌دهند، اما به طور گسترده قابل اجرا هستند و بنابراین برای طیف گسترده‌ای از مسائل افزایش سرعت می‌دهند. [22]

شبیه سازی سیستم های کوانتومی [ ویرایش ]

مقاله اصلی: شبیه سازی کوانتومی

از آنجایی که شیمی و نانوتکنولوژی بر درک سیستم‌های کوانتومی تکیه دارند و شبیه‌سازی چنین سیستم‌هایی به روش کلاسیک غیرممکن است، شبیه‌سازی کوانتومی ممکن است یکی از کاربردهای مهم محاسبات کوانتومی باشد. [65] شبیه‌سازی کوانتومی همچنین می‌تواند برای شبیه‌سازی رفتار اتم‌ها و ذرات در شرایط غیرعادی مانند واکنش‌های داخل یک برخورد دهنده استفاده شود . [66] در ژوئن 2023، دانشمندان کامپیوتر IBM گزارش دادند که یک کامپیوتر کوانتومی نتایج بهتری را برای یک مسئله فیزیک نسبت به یک ابرکامپیوتر معمولی تولید می‌کند. [67] [68]

حدود 2 درصد از تولید انرژی جهانی سالانه برای تثبیت نیتروژن برای تولید آمونیاک برای فرآیند هابر در صنعت کود کشاورزی استفاده می شود (حتی اگر موجودات طبیعی نیز آمونیاک تولید کنند). شبیه‌سازی‌های کوانتومی ممکن است برای درک این فرآیند و افزایش بهره‌وری انرژی تولید مورد استفاده قرار گیرند. [69] انتظار می‌رود که استفاده اولیه از محاسبات کوانتومی مدل‌سازی باشد که کارایی فرآیند هابر-بوش [70] را تا اواسط دهه 2020 بهبود می‌بخشد [71] اگرچه برخی پیش‌بینی کرده‌اند که زمان بیشتری طول خواهد کشید. [72]

رمزنگاری پس کوانتومی [ ویرایش ]

مقاله اصلی: رمزنگاری پس کوانتومی

یک کاربرد قابل توجه محاسبات کوانتومی برای حملات به سیستم های رمزنگاری است که در حال حاضر مورد استفاده قرار می گیرند. فرض بر این است که فاکتورسازی اعداد صحیح ، که زیربنای امنیت سیستم های رمزنگاری کلید عمومی است، با یک کامپیوتر معمولی برای اعداد صحیح بزرگ از نظر محاسباتی غیرممکن است، اگر حاصل ضرب اعداد اول معدود (مثلاً محصول دو عدد اول 300 رقمی) باشند. [73] در مقایسه، یک کامپیوتر کوانتومی می‌تواند با استفاده از الگوریتم شور برای یافتن عوامل آن، این مشکل را با سرعت بیشتری حل کند . [74] این توانایی به یک کامپیوتر کوانتومی اجازه می‌دهد تا بسیاری از سیستم‌های رمزنگاری مورد استفاده امروزی را بشکند، به این معنا که یک الگوریتم زمان چند جمله‌ای (به تعداد ارقام عدد صحیح) برای حل مسئله وجود دارد . به طور خاص، بیشتر رمزهای کلید عمومی محبوب بر اساس دشواری فاکتورگیری اعداد صحیح یا مسئله لگاریتم گسسته است که هر دوی آنها را می توان با الگوریتم Shor حل کرد. به طور خاص، الگوریتم‌های RSA ، Diffie–Hellman ، و منحنی بیضوی Diffie–Hellman می‌توانند شکسته شوند. این ها برای محافظت از صفحات وب ایمن، ایمیل های رمزگذاری شده و بسیاری از انواع دیگر داده ها استفاده می شوند. شکستن این موارد پیامدهای قابل توجهی برای حفظ حریم خصوصی و امنیت الکترونیکی خواهد داشت.

شناسایی سیستم های رمزنگاری که ممکن است در برابر الگوریتم های کوانتومی ایمن باشند، موضوعی است که به طور فعال در زمینه رمزنگاری پس کوانتومی تحقیق شده است . [75] [76] برخی از الگوریتم‌های کلید عمومی مبتنی بر مسائلی غیر از فاکتورسازی اعداد صحیح و مسائل لگاریتمی گسسته هستند که الگوریتم Shor برای آنها اعمال می‌شود، مانند سیستم رمزگذاری McEliece بر اساس مشکلی در نظریه کدگذاری . [75] [77] سیستم‌های رمزنگاری مبتنی بر شبکه همچنین شناخته شده نیستند که توسط رایانه‌های کوانتومی شکسته شوند، و یافتن یک الگوریتم زمانی چند جمله‌ای برای حل مشکل زیرگروه پنهان دووجهی ، که می‌تواند بسیاری از سیستم‌های رمزنگاری مبتنی بر شبکه را بشکند، یک مسئله باز است که به خوبی مطالعه شده است. . [78] ثابت شده است که استفاده از الگوریتم گروور برای شکستن یک الگوریتم متقارن (کلید مخفی) با نیروی بی رحم به زمان برابر با تقریباً 2 n / 2 فراخوانی الگوریتم رمزنگاری زیربنایی در مقایسه با تقریباً 2 n در حالت کلاسیک نیاز دارد . 79] به این معنی که طول کلید متقارن به طور مؤثر نصف می‌شود: AES-256 در برابر حمله با استفاده از الگوریتم گروور دارای همان امنیت است که AES-128 در برابر جستجوی کلاسیک با نیروی brute-force دارد (به اندازه کلید مراجعه کنید ).

مشکلات جستجو[ ویرایش ]

مقاله اصلی: الگوریتم گروور

معروف‌ترین مثال از مسئله‌ای که امکان افزایش سرعت کوانتومی چند جمله‌ای را فراهم می‌کند، جستجوی بدون ساختار است که شامل یافتن یک آیتم علامت‌گذاری شده از یک لیست است.� $n$ موارد موجود در پایگاه داده این را می توان با استفاده از الگوریتم گروور حل کرد�(�) $O({\sqrt {n}})$ پرس و جو به پایگاه داده، درجه دوم کمتر ازΩ(�) $\Omega (n)$ پرس و جوهای مورد نیاز برای الگوریتم های کلاسیک در این مورد، مزیت نه تنها قابل اثبات است، بلکه بهینه است: نشان داده شده است که الگوریتم گروور حداکثر احتمال ممکن را برای یافتن عنصر مورد نظر برای هر تعداد جستجوی اوراکل می دهد. نمونه‌های زیادی از سرعت‌های کوانتومی قابل اثبات برای مسائل پرس و جو بر اساس الگوریتم گروور است، از جمله الگوریتم Brassard، Høyer و Tapp برای یافتن برخورد در توابع دو به یک، [80] و الگوریتم Farhi، Goldstone و Gutmann برای ارزیابی درختان NAND. [81]

مسائلی که می توانند به طور موثر با الگوریتم گروور مورد بررسی قرار گیرند دارای ویژگی های زیر هستند: [82] [83]

هیچ ساختار قابل جستجو در مجموعه پاسخ های ممکن وجود ندارد،
تعداد پاسخ‌های ممکن برای بررسی برابر با تعداد ورودی‌های الگوریتم است و
یک تابع بولی وجود دارد که هر ورودی را ارزیابی می کند و تعیین می کند که آیا پاسخ صحیح است یا خیر.

برای مسائل مربوط به همه این ویژگی ها، زمان اجرای الگوریتم گروور در یک کامپیوتر کوانتومی به عنوان جذر تعداد ورودی ها (یا عناصر در پایگاه داده) در مقایسه با مقیاس خطی الگوریتم های کلاسیک مقیاس می شود. یک دسته کلی از مسائل که الگوریتم گروور را می توان برای آنها اعمال کرد [84] یک مسئله رضایت پذیری بولی است ، که در آن پایگاه داده ای که الگوریتم از طریق آن تکرار می شود، تمام پاسخ های ممکن است. یک مثال و کاربرد احتمالی آن یک رمز عبور است که سعی در حدس زدن رمز عبور دارد. شکستن رمزهای متقارن با این الگوریتم مورد توجه سازمان های دولتی است. [85]

آنیل کوانتومی[ ویرایش ]

بازپخت کوانتومی برای انجام محاسبات به قضیه آدیاباتیک متکی است. یک سیستم در حالت پایه برای یک همیلتونی ساده قرار می گیرد که به آرامی به یک هامیلتونی پیچیده تر تبدیل می شود که حالت پایه آن نشان دهنده راه حل مسئله مورد نظر است. قضیه آدیاباتیک بیان می کند که اگر تکامل به اندازه کافی کند باشد، سیستم همیشه در طول فرآیند در حالت پایه خود باقی می ماند.بهینه سازی آدیاباتیک ممکن است برای حل مسائل زیست شناسی محاسباتی مفید باشد . [86]

یادگیری ماشینی [ ویرایش ]

مقاله اصلی: یادگیری ماشین کوانتومی

از آنجایی که رایانه‌های کوانتومی می‌توانند خروجی‌هایی تولید کنند که رایانه‌های کلاسیک نمی‌توانند به طور مؤثر تولید کنند، و از آنجایی که محاسبات کوانتومی اساساً جبری خطی است، برخی به توسعه الگوریتم‌های کوانتومی که می‌توانند وظایف یادگیری ماشین را سرعت بخشند، ابراز امیدواری می‌کنند . [87] [34]

به عنوان مثال، الگوریتم کوانتومی برای سیستم های معادلات خطی ، یا "الگوریتم HHL" که به نام کاشفان آن هارو، هاسیدیم و لوید نامگذاری شده است، اعتقاد بر این است که سرعت بیشتری را نسبت به همتایان کلاسیک ارائه می دهد. [88] [34] برخی از گروه‌های تحقیقاتی اخیراً استفاده از سخت‌افزار آنیل کوانتومی را برای آموزش ماشین‌های بولتزمن و شبکه‌های عصبی عمیق بررسی کرده‌اند . [89] [90] [91]

مدل های شیمی مولد عمیق به عنوان ابزار قدرتمندی برای تسریع در کشف دارو ظاهر می شوند . با این حال، اندازه و پیچیدگی بسیار زیاد فضای ساختاری همه مولکول‌های احتمالی شبیه دارو، موانع مهمی را ایجاد می‌کند که می‌توان در آینده توسط رایانه‌های کوانتومی بر آنها غلبه کرد. کامپیوترهای کوانتومی به طور طبیعی برای حل مسائل پیچیده کوانتومی چند جسمی [23] خوب هستند و بنابراین ممکن است در کاربردهای مربوط به شیمی کوانتومی مفید باشند. بنابراین، می‌توان انتظار داشت که مدل‌های مولد کوانتومی [92] از جمله GAN‌های کوانتومی [93] ممکن است در نهایت به الگوریتم‌های شیمی مولد نهایی تبدیل شوند.

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:0 توسط علی رضا نقش |

2-محاسبات کوانتومی

اپراتورهای واحد[ ویرایش ]

همچنین ببینید: واحد (فیزیک)

وضعیت این حافظه کوانتومی یک کیوبیتی را می‌توان با استفاده از گیت‌های منطقی کوانتومی ، مشابه نحوه دستکاری حافظه کلاسیک با گیت‌های منطقی کلاسیک، دستکاری کرد . یکی از دروازه های مهم برای محاسبات کلاسیک و کوانتومی، دروازه NOT است که می تواند با یک ماتریس نمایش داده شود.

${\displaystyle X:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.$

از نظر ریاضی، استفاده از چنین دروازه منطقی برای بردار حالت کوانتومی با ضرب ماتریس مدل‌سازی می‌شود . بدین ترتیب

$X|0\rangle =|1\rangle$ و $X|1\rangle =|0\rangle$ .

ریاضیات دروازه‌های تک کیوبیتی را می‌توان به دو روش مهم برای کار بر روی حافظه‌های کوانتومی چند کیوبیتی گسترش داد. یک راه این است که به سادگی یک کیوبیت را انتخاب کنید و آن گیت را روی کیوبیت هدف اعمال کنید و در عین حال باقیمانده حافظه را بی‌تأثیر بگذارید. راه دیگر این است که تنها در صورتی که بخش دیگری از حافظه در وضعیت دلخواه باشد، گیت را روی هدف خود اعمال کنید. این دو انتخاب را می توان با استفاده از مثال دیگری نشان داد. حالت های ممکن یک حافظه کوانتومی دو کیوبیتی هستند

${\displaystyle |00\rangle :={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\quad |01\rangle :={\begin{pmatrix}0\\1 \\0\\0\end{pmatrix}};\quad |10\rangle :={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\quad |11\rangle :={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}.$

سپس گیت کنترل شده NOT (CNOT) را می توان با استفاده از ماتریس زیر نشان داد:

${\displaystyle \operatorname {CNOT} :={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}}.$

به عنوان یک نتیجه ریاضی این تعریف، ${\textstyle \operatorname {CNOT} |00\rangle =|00\rangle }$ ، ${\textstyle \operatorname {CNOT} |01\rangle =|01\rangle }$ ، ${\textstyle \operatorname {CNOT} |10\rangle =|11\rangle }$ ، و ${\textstyle \operatorname {CNOT} |11\rangle =|10\rangle }$ . به عبارت دیگر، CNOT یک گیت NOT را اعمال می کند ${\textstyle X}$ از قبل) به کیوبیت دوم اگر و فقط اگر کیوبیت اول در حالت باشد ${\textstyle |1\rangle }$ . اگر کیوبیت اول باشد ${\textstyle |0\rangle }$ ، برای هیچ کدام از کیوبیت ها کاری انجام نمی شود.

به طور خلاصه، محاسبات کوانتومی را می توان به عنوان شبکه ای از گیت ها و اندازه گیری های منطق کوانتومی توصیف کرد. با این حال، هر اندازه‌گیری را می‌توان به پایان محاسبات کوانتومی موکول کرد ، اگرچه این تعویق ممکن است هزینه محاسباتی داشته باشد، بنابراین بیشتر مدارهای کوانتومی شبکه‌ای را نشان می‌دهند که فقط از گیت‌های منطقی کوانتومی تشکیل شده است و هیچ اندازه‌گیری ندارد.

توازی کوانتومی [ ویرایش ]

توازی کوانتومی اکتشافی است که کامپیوترهای کوانتومی را می توان به عنوان ارزیابی یک تابع برای مقادیر ورودی چندگانه به طور همزمان در نظر گرفت. این را می توان با تهیه یک سیستم کوانتومی در برهم نهی از حالات ورودی، و اعمال یک تبدیل واحد که تابع مورد ارزیابی را رمزگذاری می کند، به دست آورد. حالت حاصل، مقادیر خروجی تابع را برای همه مقادیر ورودی در برهم نهی رمزگذاری می‌کند و امکان محاسبه خروجی‌های متعدد را به طور همزمان فراهم می‌کند. این ویژگی کلید افزایش سرعت بسیاری از الگوریتم های کوانتومی است. با این حال، "موازی" در این معنا برای سرعت بخشیدن به محاسبات کافی نیست، زیرا اندازه گیری در پایان محاسبات تنها یک مقدار می دهد. برای مفید بودن، یک الگوریتم کوانتومی باید برخی از اجزای مفهومی دیگر را نیز در خود جای دهد. [49] [50]

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 7:58 توسط علی رضا نقش |

1-محاسبات کوانتومی

از ویکیپدیا، دانشنامه آزاد

IBM Q System One ، یک کامپیوتر کوانتومی با 20 کیوبیت ابررسانا [1]

کامپیوتر کوانتومی کامپیوتری است که از پدیده های مکانیک کوانتومی بهره می برد .

در مقیاس‌های کوچک، ماده فیزیکی خواص ذرات و امواج را نشان می‌دهد و محاسبات کوانتومی از این رفتار، به‌ویژه برهم‌نهی و درهم‌تنیدگی کوانتومی، با استفاده از سخت‌افزار تخصصی که از آماده‌سازی و دستکاری حالت‌های کوانتومی پشتیبانی می‌کند، استفاده می‌کند .

فیزیک کلاسیک نمی‌تواند عملکرد این دستگاه‌های کوانتومی را توضیح دهد، و یک کامپیوتر کوانتومی مقیاس‌پذیر می‌تواند برخی از محاسبات را به‌طور تصاعدی سریع‌تر (با توجه به مقیاس‌گذاری اندازه ورودی) [2] از هر رایانه مدرن «کلاسیک» انجام دهد . به طور خاص، یک کامپیوتر کوانتومی در مقیاس بزرگ می تواند طرح های رمزگذاری پرکاربرد را بشکند و به فیزیکدانان در انجام شبیه سازی های فیزیکی کمک کند . با این حال، وضعیت فعلی هنر تا حد زیادی تجربی و غیر عملی است، با موانع متعددی برای کاربردهای مفید. علاوه بر این، رایانه‌های کوانتومی مقیاس‌پذیر برای بسیاری از کارهای عملی نویدبخش نیستند، و برای بسیاری از کارهای مهم افزایش سرعت کوانتومی غیرممکن است.

واحد اصلی اطلاعات در محاسبات کوانتومی کیوبیت است ، مشابه بیت در الکترونیک دیجیتال سنتی. برخلاف یک بیت کلاسیک، یک کیوبیت می تواند در برهم نهی دو حالت «پایه» خود وجود داشته باشد. هنگام اندازه گیری یک کیوبیت، نتیجه یک خروجی احتمالی یک بیت کلاسیک است، بنابراین کامپیوترهای کوانتومی را به طور کلی غیر قطعی می کند. اگر یک کامپیوتر کوانتومی کیوبیت را به روشی خاص دستکاری کند، اثرات تداخل موج می تواند نتایج اندازه گیری مورد نظر را تقویت کند. طراحی الگوریتم های کوانتومی شامل ایجاد رویه هایی است که به کامپیوتر کوانتومی اجازه می دهد تا محاسبات را به طور موثر و سریع انجام دهد.

مهندسی فیزیکی کیوبیت های با کیفیت بالا چالش برانگیز است. اگر یک کیوبیت فیزیکی به اندازه کافی از محیط خود جدا نشده باشد ، دچار ناهمدوسی کوانتومی می شود که نویز را وارد محاسبات می کند. به طور متناقض، جداسازی کامل کیوبیت ها نیز نامطلوب است، زیرا محاسبات کوانتومی معمولاً نیاز به مقداردهی اولیه کیوبیت ها، انجام برهمکنش های کیوبیت کنترل شده و اندازه گیری حالت های کوانتومی حاصل دارند. هر یک از این عملیات خطاهایی را ایجاد می کند و از نویز رنج می برد و چنین نادرستی ها انباشته می شوند.

دولت‌های ملی سرمایه‌گذاری زیادی در تحقیقات تجربی انجام داده‌اند که هدف آن توسعه کیوبیت‌های مقیاس‌پذیر با زمان انسجام طولانی‌تر و نرخ خطای کمتر است. دو تا از امیدوارکننده‌ترین فناوری‌ها ابررساناها (که جریان الکتریکی را با حذف مقاومت الکتریکی جدا می‌کنند ) و تله‌های یونی (که یک یون را با استفاده از میدان‌های الکترومغناطیسی محدود می‌کنند ) هستند.

در اصل، یک کامپیوتر غیرکوانتومی (کلاسیک) می‌تواند مشکلات محاسباتی مشابه یک کامپیوتر کوانتومی را با توجه به زمان کافی حل کند. مزیت کوانتومی به‌جای محاسبه‌پذیری، به شکل پیچیدگی زمانی است ، و نظریه پیچیدگی کوانتومی نشان می‌دهد که برخی از الگوریتم‌های کوانتومی برای کارهایی که با دقت انتخاب شده‌اند به مراحل محاسباتی نمایی کمتری نسبت به بهترین الگوریتم‌های غیرکوانتومی شناخته‌شده نیاز دارند. چنین کارهایی در تئوری می توانند بر روی یک کامپیوتر کوانتومی در مقیاس بزرگ حل شوند، در حالی که کامپیوترهای کلاسیک محاسبات را در هیچ زمان معقولی به پایان نمی‌رسانند. با این حال، سرعت کوانتومی جهانی یا حتی معمولی در بین وظایف محاسباتی نیست، زیرا ثابت شده است که کارهای اساسی مانند مرتب‌سازی اجازه هیچ سرعت کوانتومی مجانبی را نمی‌دهند. ادعاهای برتری کوانتومی توجه قابل توجهی را به این رشته جلب کرده است، اما در کارهای ساختگی نشان داده شده است، در حالی که موارد استفاده عملی کوتاه مدت محدود باقی مانده است.

خوش‌بینی در مورد محاسبات کوانتومی توسط طیف گسترده‌ای از امکانات سخت‌افزار نظری جدید که توسط فیزیک کوانتومی تسهیل شده است، تقویت می‌شود ، اما درک بهتر از محدودیت‌های محاسبات کوانتومی این خوش‌بینی را متعادل می‌کند. به طور خاص، سرعت‌های کوانتومی به طور سنتی برای رایانه‌های کوانتومی بدون نویز تخمین زده می‌شود، در حالی که تأثیر نویز و استفاده از تصحیح خطای کوانتومی می‌تواند سرعت‌های چندجمله‌ای پایین را تضعیف کند.

تاریخچه [ ویرایش ]

برای راهنمای زمانی، جدول زمانی محاسبات کوانتومی و ارتباطات را ببینید .

تداخل سنج ماخ -زندر نشان می دهد که فوتون ها می توانند تداخل موج مانندی از خود نشان دهند .

برای سال‌های متمادی، رشته‌های مکانیک کوانتومی و علوم کامپیوتر جوامع دانشگاهی مجزایی را تشکیل دادند. [3] نظریه کوانتومی مدرن در دهه 1920 توسعه یافت تا دوگانگی موج-ذره مشاهده شده در مقیاس اتمی را توضیح دهد، [4] و رایانه های دیجیتال در دهه های بعدی به وجود آمدند تا جایگزین رایانه های انسانی برای محاسبات خسته کننده شوند. [5] هر دو رشته در طول جنگ جهانی دوم کاربردهای عملی داشتند . کامپیوترها نقش مهمی در رمزنگاری زمان جنگ داشتند ، [6] و فیزیک کوانتومی برای فیزیک هسته ای مورد استفاده در پروژه منهتن ضروری بود . [7]

همانطور که فیزیکدانان مدل های مکانیکی کوانتومی را برای مسائل محاسباتی به کار بردند و بیت های دیجیتال را با کیوبیت ها تعویض کردند ، زمینه های مکانیک کوانتومی و علوم کامپیوتر شروع به همگرایی کردند. در سال 1980، پل بنیوف ماشین تورینگ کوانتومی را معرفی کرد که از نظریه کوانتومی برای توصیف یک کامپیوتر ساده شده استفاده می کند. [8] هنگامی که رایانه‌های دیجیتال سریع‌تر شدند، فیزیکدانان هنگام شبیه‌سازی دینامیک کوانتومی با افزایش نمایی در سربار مواجه شدند ، [9] که یوری مانین و ریچارد فاینمن را وادار کرد تا به طور مستقل پیشنهاد کنند که سخت‌افزار مبتنی بر پدیده‌های کوانتومی ممکن است برای شبیه‌سازی رایانه‌ای کارآمدتر باشد. [10] [11] [12] در مقاله ای در سال 1984، چارلز بنت و ژیل براسارد نظریه کوانتومی را برای پروتکل های رمزنگاری به کار بردند و نشان دادند که توزیع کلید کوانتومی می تواند امنیت اطلاعات را افزایش دهد . [13] [14]

پیتر شور (تصویر اینجا در سال 2017) در سال 1994 نشان داد که یک کامپیوتر کوانتومی مقیاس پذیر می تواند رمزگذاری RSA را بشکند .

سپس الگوریتم‌های کوانتومی برای حل مسائل اوراکل ظاهر شدند ، مانند الگوریتم دویچ در سال 1985، [15] الگوریتم برنشتاین-وزیرانی در سال 1993، [ 16] و الگوریتم سیمون در سال 1994. می توان اطلاعات بیشتری را با پرس و جو از یک جعبه سیاه با حالت کوانتومی در برهم نهی بدست آورد که گاهی اوقات به آن موازی سازی کوانتومی می گویند . [18] پیتر شور با الگوریتم‌های سال 1994 خود برای شکستن پروتکل‌های رمزگذاری پرکاربرد RSA و Diffie-Hellman ، [19] که توجه قابل توجهی را به حوزه محاسبات کوانتومی جلب کرد، بر این نتایج بنا نهاد . [20] در سال 1996، الگوریتم گروور یک افزایش سرعت کوانتومی را برای مشکل جستجوی بدون ساختار به طور گسترده ای ایجاد کرد . [21] [22] در همان سال، ست لوید ثابت کرد که رایانه‌های کوانتومی می‌توانند سیستم‌های کوانتومی را بدون سربار نمایی موجود در شبیه‌سازی‌های کلاسیک شبیه‌سازی کنند، [23] که حدس فاینمن در سال 1982 را تأیید کرد. [24]

در طول سال‌ها، آزمایش‌گران کامپیوترهای کوانتومی در مقیاس کوچک را با استفاده از یون‌های به دام افتاده و ابررساناها ساخته‌اند . [25] در سال 1998، یک کامپیوتر کوانتومی دو کیوبیت امکان‌سنجی این فناوری را نشان داد، [26] [27] و آزمایش‌های بعدی تعداد کیوبیت‌ها را افزایش داده و نرخ خطا را کاهش داد. [25] در سال 2019، هوش مصنوعی گوگل و ناسا اعلام کردند که با یک ماشین 54 کیوبیتی به برتری کوانتومی دست یافته‌اند و محاسباتی را انجام می‌دهند که برای هر کامپیوتر کلاسیک غیرممکن است. [28] [29] [30] با این حال، اعتبار این ادعا هنوز به طور فعال در حال تحقیق است. [31] [32]

قضیه آستانه نشان می‌دهد که چگونه افزایش تعداد کیوبیت‌ها می‌تواند خطاها را کاهش دهد، [33] اما محاسبات کوانتومی کاملاً متحمل خطا «یک رویای نسبتاً دور» باقی می‌ماند. [34] به گفته برخی از محققان، ماشین‌های کوانتومی مقیاس متوسط پر سر و صدا ( NISQ ) ممکن است در آینده نزدیک کاربردهای تخصصی داشته باشند، اما نویز در دروازه‌های کوانتومی قابلیت اطمینان آنها را محدود می‌کند. [34]

سرمایه گذاری در تحقیقات محاسبات کوانتومی در بخش های دولتی و خصوصی افزایش یافته است. [35] [36] همانطور که یک شرکت مشاوره خلاصه کرد، [37]

با تمرکز بر دیدگاه مدیریت کسب و کار، کاربردهای بالقوه محاسبات کوانتومی در چهار دسته اصلی عبارتند از: امنیت سایبری، تجزیه و تحلیل داده ها و هوش مصنوعی، بهینه سازی و شبیه سازی، و مدیریت و جستجوی داده ها. [38]

در دسامبر 2023، فیزیکدانان، برای اولین بار، درهم تنیدگی مولکول های منفرد را گزارش کردند، که ممکن است کاربردهای قابل توجهی در محاسبات کوانتومی داشته باشد. [39] همچنین در دسامبر 2023، دانشمندان در هاروارد با موفقیت "مدارهای کوانتومی" را ایجاد کردند که خطاها را با کارآمدی بهتری نسبت به روش های جایگزین تصحیح می کند، که ممکن است به طور بالقوه مانع بزرگی را برای رایانه های کوانتومی عملی از بین ببرد. [40] [41] تیم تحقیقاتی هاروارد توسط MIT ، QuEra Computing ، Caltech ، و پرینستون پشتیبانی شد و توسط برنامه بهینه‌سازی دارپا با دستگاه‌های کوانتومی مقیاس متوسط نویز (ONISQ) تامین مالی شد. [42] [43]

پردازش اطلاعات کوانتومی [ ویرایش ]

همچنین ببینید: مقدمه ای بر مکانیک کوانتومی

مهندسان کامپیوتر معمولاً عملکرد یک کامپیوتر مدرن را بر حسب الکترودینامیک کلاسیک توصیف می کنند . در این رایانه‌های «کلاسیک»، برخی از مؤلفه‌ها (مانند نیمه رساناها و مولدهای اعداد تصادفی ) ممکن است به رفتار کوانتومی متکی باشند، اما این مؤلفه‌ها از محیط خود جدا نیستند ، بنابراین هر اطلاعات کوانتومی به سرعت از هم جدا می‌شود . در حالی که برنامه نویسان ممکن است هنگام طراحی یک الگوریتم تصادفی به نظریه احتمال وابسته باشند ، مفاهیم مکانیکی کوانتومی مانند برهم نهی و تداخل تا حد زیادی برای تجزیه و تحلیل برنامه بی ربط هستند .

در مقابل، برنامه های کوانتومی بر کنترل دقیق سیستم های کوانتومی منسجم متکی هستند . فیزیکدانان این سیستم ها را به صورت ریاضی با استفاده از جبر خطی توصیف می کنند . اعداد مختلط دامنه‌های احتمال را مدل‌سازی می‌کنند ، بردارها حالت‌های کوانتومی را مدل می‌کنند و ماتریس‌ها عملیاتی را که می‌توان روی این حالت‌ها انجام داد، مدل‌سازی می‌کنند. سپس برنامه نویسی یک کامپیوتر کوانتومی عبارت است از ترکیب عملیات به گونه ای که برنامه به دست آمده یک نتیجه مفید را در تئوری محاسبه کند و در عمل قابل اجرا باشد.

همانطور که فیزیکدان چارلی بنت رابطه بین کامپیوترهای کوانتومی و کلاسیک را توصیف می کند، [44]

یک کامپیوتر کلاسیک یک کامپیوتر کوانتومی است ... بنابراین ما نباید بپرسیم که "سرعت های کوانتومی از کجا می آیند؟" ما باید بگوییم، "خب، همه کامپیوترها کوانتومی هستند... کندی های کلاسیک از کجا می آیند؟"

اطلاعات کوانتومی [ ویرایش ]

همانطور که بیت مفهوم اصلی نظریه اطلاعات کلاسیک است، کیوبیت نیز واحد اساسی اطلاعات کوانتومی است . همان اصطلاح کیوبیت برای اشاره به یک مدل ریاضی انتزاعی و به هر سیستم فیزیکی که توسط آن مدل نشان داده می شود استفاده می شود. یک بیت کلاسیک، طبق تعریف، در هر یک از دو حالت فیزیکی وجود دارد که می‌توان آن‌ها را 0 و 1 نشان داد. یک کیوبیت نیز با یک حالت توصیف می‌شود و دو حالت اغلب نوشته می‌شوند |0〉 و |1〉 به عنوان همتای کوانتومی عمل می‌کنند. حالات کلاسیک 0 و 1. با این حال، حالات کوانتومی |0〉 و |1〉 متعلق به یک فضای برداری هستند ، به این معنی که می توان آنها را در ثابت ضرب کرد و با هم جمع کرد و نتیجه دوباره یک حالت کوانتومی معتبر است. چنین ترکیبی به عنوان برهم نهی |0〉 و |1〉 شناخته می شود . [45] [46]

یک بردار دو بعدی از نظر ریاضی یک حالت کیوبیت را نشان می دهد. فیزیکدانان معمولاً از نماد دیراک برای جبر خطی مکانیک کوانتومی استفاده می کنند ψ 〉 ' ket psi ' برای بردار با برچسب ψ . از آنجایی که کیوبیت یک سیستم دو حالته است، هر حالت کیوبیت به شکل α |0〉 + β |1〉 است ، که در آن |0〉 و |1〉 حالت های پایه استاندارد هستند ، [a] و α و β احتمال هستند. دامنه ها که در اعداد مختلط کلی هستند . [46] اگر α یا β صفر باشد، کیوبیت در واقع یک بیت کلاسیک است. وقتی هر دو غیر صفر هستند، کیوبیت در برهم نهی است. چنین بردار حالت کوانتومی مشابه بردار احتمال (کلاسیک) عمل می کند ، با یک تفاوت کلیدی: برخلاف احتمالات، دامنه های احتمال لزوماً اعداد مثبت نیستند. [48] دامنه های منفی اجازه تداخل موج مخرب را می دهد.

هنگامی که یک کیوبیت بر اساس استاندارد اندازه گیری می شود ، نتیجه یک بیت کلاسیک است. قانون Born مطابقت مربع هنجار بین دامنه ها و احتمالات را توصیف می کند - هنگام اندازه گیری یک کیوبیت α |0〉 + β |1〉 ، حالت به |0〉 با احتمال | α | 2 یا به |1〉 با احتمال | β | 2 . هر حالت کیوبیت معتبر دارای ضرایب α و β است به طوری که | α | 2 + | β | 2 = 1 . به عنوان مثال، اندازه گیری کیوبیت1/√2|0〉 +1/√2|1〉 یا |0〉 یا |1〉 با احتمال مساوی تولید می کند.

هر کیوبیت اضافی بعد فضای حالت را دو برابر می کند . [47] به عنوان مثال، بردار1/√2|00〉 +1/√2|01〉 یک حالت دو کیوبیتی، حاصل ضرب تانسور کیوبیت |0〉 با کیوبیت را1/√2|0〉 +1/√2|1〉 . این بردار در فضای برداری چهاربعدی قرار داردکه بردارهای پایه |00〉 ، |01〉 ، |10〉 ، و |11〉 پوشانده شده است . ایالت بل 1/√2|00〉 +1/√2|11〉 غیرممکن است که به حاصل ضرب تانسور دو کیوبیت منفرد تجزیه شود - این دو کیوبیت درهم تنیده هستند زیرا دامنه احتمال آنها همبسته است . به طور کلی، فضای برداری برای یکسیستم n -qubit 2n بعدی است، و این امر شبیه سازی یک کوانتومی را برای یک کامپیوتر کلاسیک چالش برانگیز می کند: نمایش یک سیستم 100 کیوبیتی مستلزم ذخیره 2100 مقدار کلاسیک است.

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 7:51 توسط علی رضا نقش |

آموزش

کاربرد یادگیری کلاسیک در مسائل کوانتومی [ ویرایش ]

نظریه یادگیری کوانتومی [ ویرایش ]

پیاده سازی و آزمایش [ ویرایش ]

شک و تردید [ ویرایش ]

همچنین ببینید [ ویرایش ]

منبع

تکنیک های نمونه برداری کوانتومی [ ویرایش ]

شبکه های عصبی کوانتومی [ ویرایش ]

شبکه عصبی کانولوشن کوانتومی [ ویرایش ]

مدل‌های مارکوف کوانتومی پنهان [ ویرایش ]

یادگیری ماشین کاملاً کوانتومی [ ویرایش ]

یادگیری ماشین کوانتومی قابل توضیح [ ویرایش ]

یادگیری ماشین با کامپیوترهای کوانتومی [ ویرایش ]

حافظه های انجمنی کوانتومی و تشخیص الگوی کوانتومی [ ویرایش ]

شبیه سازی جبر خطی با دامنه های کوانتومی [ ویرایش ]

الگوریتم های کوانتومی متغیر (VQAs) [ ویرایش ]

مدارهای کوانتومی متغیر (VQCs) [ ویرایش ]

طبقه بندی کننده باینری کوانتومی [ ویرایش ]

الگوریتم های یادگیری ماشین کوانتومی بر اساس جستجوی گروور [ ویرایش ]

یادگیری تقویتی کوانتومی [ ویرایش ]

آنیل کوانتومی [ ویرایش ]

مدار NISQ به عنوان مدل کوانتومی [ ویرایش ]

پس زمینه [ ویرایش ]

مدل محاسباتی [ ویرایش ]

محاسبات مکانیکی [ ویرایش ]

محاسبات آنالوگ [ ویرایش ]

کامپیوترهای دیجیتال الکترونیکی [ ویرایش ]

رویکردهای عمومی [ ویرایش ]

اشیاء فیزیکی [ ویرایش ]

محاسبات مخزن [ ویرایش ]

محاسبات ملموس [ ویرایش ]

محاسبات انسانی [ ویرایش ]

تعامل انسان و ربات [ ویرایش ]

محاسبات ازدحام [ ویرایش ]

رویکردهای فیزیک [ ویرایش ]

محاسبات نوری [ ویرایش ]

اسپینترونیکس [ ویرایش ]

اتمترونیک [ ویرایش ]

سیالات [ ویرایش ]

محاسبات کوانتومی [ ویرایش ]

محاسبات ابررسانا [ ویرایش ]

سیستم های میکروالکترومکانیکی [ ویرایش ]

رویکردهای شیمی [ ویرایش ]

محاسبات مولکولی [ ویرایش ]

رویکردهای بیوشیمی [ ویرایش ]

محاسبات پپتید [ ویرایش ]

محاسبات DNA [ ویرایش ]

محاسبات غشایی [ ویرایش ]

رویکردهای بیولوژیکی [ ویرایش ]

علوم اعصاب [ ویرایش ]

اتوماتای ​​سلولی و محاسبات آمورف [ ویرایش ]

محاسبات تکاملی [ ویرایش ]

رویکردهای ریاضی [ ویرایش ]

محاسبات سه تایی [ ویرایش ]

محاسبات برگشت پذیر [ ویرایش ]

محاسبات آشوب [ ویرایش ]

محاسبات تصادفی [ ویرایش ]

همچنین ببینید [ ویرایش ]

منبع

نامزدهای تحقق فیزیکی [ ویرایش ]

تئوری[ ویرایش ]

محاسبه پذیری[ ویرایش ]

پیچیدگی[ ویرایش ]

همچنین ببینید [ ویرایش ]

https://en.wikipedia.org/wiki/Quantum_computing

مهندسی[ ویرایش ]

چالش ها [ ویرایش ]

برتری کوانتومی [ ویرایش ]

شک و تردید [ ویرایش ]

برنامه نویسی کوانتومی[ ویرایش ]

ارتباطات [ ویرایش ]

الگوریتم ها [ ویرایش ]

شبیه سازی سیستم های کوانتومی [ ویرایش ]

رمزنگاری پس کوانتومی [ ویرایش ]

مشکلات جستجو[ ویرایش ]

آنیل کوانتومی[ ویرایش ]

یادگیری ماشینی [ ویرایش ]

اپراتورهای واحد[ ویرایش ]

توازی کوانتومی [ ویرایش ]

اتوماتای سلولی و محاسبات آمورف [ ویرایش ]