2-شناخت کوانتومی
بازنمایی دانش [ ویرایش ]
مفاهیم پدیده های شناختی اساسی هستند که محتوایی را برای استنتاج، توضیح و درک زبان فراهم می کنند. روانشناسی شناختی رویکردهای متفاوتی را برای درک مفاهیم از جمله نمونهها، نمونههای اولیه و شبکههای عصبی مورد تحقیق قرار داده است و مشکلات اساسی مختلفی مانند رفتار غیر کلاسیک آزمایششده تجربی برای پیوند و تفکیک مفاهیم، بهویژه مسئله Pet-Fish یا Pet-Fish شناسایی شده است. اثر گوپی، [34] و گسترش بیش از حد و کمتر از حد معمول بودن و وزن عضویت برای ربط و تفکیک. [35] [36] به طور کلی، شناخت کوانتومی به سه روش برای مدلسازی مفاهیم از نظریه کوانتومی استفاده کرده است.
- از زمینهای بودن نظریه کوانتومی برای توضیح زمینهای بودن مفاهیم در شناخت و زبان و پدیده ویژگیهای نوظهور هنگام ترکیب مفاهیم استفاده کنید [11] [37] [38] [39] [40]
- از درهم تنیدگی کوانتومی برای مدلسازی معنایی ترکیبهای مفاهیم به روشی غیرتجزیهای، و به حساب آوردن ویژگیها/همبستگان/استنتاجهای نوظهور در رابطه با ترکیبهای مفهومی استفاده کنید [41]
- از برهم نهی کوانتومی برای توضیح ظهور یک مفهوم جدید در هنگام ترکیب مفاهیم استفاده کنید ، و در نتیجه یک مدل توضیحی برای وضعیت مشکل Pet-Fish، و گسترش بیش از حد و زیر بسط وزن عضویت برای پیوند و تفکیک مفاهیم ارائه دهید. [29] [37] [38]
حجم زیادی از داده های جمع آوری شده توسط همپتون [35] [36] در مورد ترکیب دو مفهوم را می توان در یک چارچوب نظری کوانتومی خاص در فضای فوک مدل سازی کرد که در آن انحرافات مشاهده شده از نظریه مجموعه کلاسیک (مجموعه فازی)، موارد فوق الذکر افزایش بیش از حد و کمتر وزنهای عضویت، از نظر تعاملات متنی، برهمنهی، تداخل، درهمتنیدگی و ظهور توضیح داده میشوند. [29] [42] [43] [44] و، بیشتر، یک آزمون شناختی بر روی یک ترکیب مفهومی خاص انجام شده است که به طور مستقیم، از طریق نقض نابرابریهای بل، درهم تنیدگی کوانتومی بین مفاهیم مؤلفه را نشان میدهد. [45] [46]
تحلیل معنایی و بازیابی اطلاعات [ ویرایش ]
تحقیق در (IV) تأثیر عمیقی بر درک و توسعه اولیه یک فرمالیسم برای به دست آوردن اطلاعات معنایی در هنگام برخورد با مفاهیم، ترکیبات آنها و زمینه های متغیر در مجموعه ای از اسناد بدون ساختار داشت. این معمای پردازش زبان طبیعی (NLP) و بازیابی اطلاعات (IR) در وب - و به طور کلی پایگاه های داده - را می توان با استفاده از فرمالیسم ریاضی نظریه کوانتومی حل کرد. به عنوان مراحل اساسی، (الف) K. Van Rijsbergen یک رویکرد ساختار کوانتومی را برای IR معرفی کرد، [47] (ب) Widdows و Peters از یک نفی منطقی کوانتومی برای یک سیستم جستجوی مشخص استفاده کردند، [40] [48] و Aerts و Czachor شناسایی کردند. ساختار کوانتومی در نظریه های فضای معنایی، مانند تحلیل معنایی نهفته . [49] از آن زمان، استفاده از تکنیک ها و رویه های ناشی از فرمالیسم های ریاضی نظریه کوانتوم - فضای هیلبرت، منطق و احتمال کوانتومی، جبرهای غیر تعویضی و غیره - در زمینه هایی مانند IR و NLP، نتایج قابل توجهی ایجاد کرده است. [50]
تاریخچه [ ویرایش ]
ایده هایی برای به کارگیری فرمالیسم های نظریه کوانتومی در شناخت اولین بار در دهه 1990 توسط دیدریک آرتس و همکارانش یان بروکارت، سونیا اسمتس و لیان گابورا توسط هارالد آتمانسپاچر، رابرت بوردلی و آندری خرنیکوف ظاهر شد. یک شماره ویژه در مورد شناخت و تصمیم کوانتومی در مجله روانشناسی ریاضی (2009، جلد 53.) ظاهر شد، که پرچمی را برای این میدان کاشت. چند کتاب مرتبط با شناخت کوانتومی منتشر شده است، از جمله کتاب های Khrennikov (2004، 2010)، Ivancivic and Ivancivic (2010)، Busemeyer and Bruza (2012)، E. Conte (2012). اولین کارگاه تعامل کوانتومی در سال 2007 در استنفورد برگزار شد که توسط پیتر بروزا، ویلیام لاولس، سی جی ون ریجسبرگن و دان سوفج به عنوان بخشی از مجموعه سمپوزیوم های بهار AAAI 2007 برگزار شد. پس از آن کارگاههایی در آکسفورد در سال 2008، زاربروکن در سال 2009، در مجموعه سمپوزیومهای پاییزی AAAI در سال 2010 برگزار شد که در واشنگتن دی سی، 2011 در آبردین ، 2012 در پاریس ، و 2013 در لستر برگزار شد . آموزش ها نیز سالانه از سال 2007 تا 2013 در نشست سالانه انجمن علوم شناختی ارائه شد . یک شماره ویژه در مورد مدل های کوانتومی شناخت در سال 2013 در مجله Topics in Cognitive Science منتشر شد .
همچنین ببینید [ ویرایش ]
- رویکردهای بیزی به عملکرد مغز - تبیین توانایی های مغز از طریق اصول آماری
- نظریه های الکترومغناطیسی آگاهی - نظریه هایی که آگاهی را به عنوان یک پدیده الکترومغناطیسی پیشنهاد می کنند
- نظریه مغز هولونومیک - تفسیر کوانتومی علوم اعصاب
- بیزییسم کوانتومی - تفسیر مکانیک کوانتومی
- منطق کوانتومی - نظریه منطق برای توضیح مشاهدات از نظریه کوانتومی
- شبکه عصبی کوانتومی – مکانیک کوانتومی در شبکه های عصبی
- NeuroQuantology – مجله علمی
- کاهش عینی هماهنگ - نظریه منشا کوانتومی آگاهی
منابع [ ویرایش ]
- ^پرش به بالا:a b Khrennikov, A. (2010). ساختار کوانتومی همه جا حاضر: از روانشناسی تا امور مالی. اسپرینگر. شابک 978-3-642-42495-3.
- ^پرش به بالا:ب Busemeyer , J.; بروزا، پ. (2012). مدل های کوانتومی شناخت و تصمیم. کمبریج: انتشارات دانشگاه کمبریج. شابک 978-1-107-01199-1.
- ^ پوتوس، EM; Busemeyer, JR (2013). "آیا احتمال کوانتومی می تواند جهت جدیدی برای مدل سازی شناختی ارائه دهد". علوم رفتاری و مغز . 36 (3): 255-274. doi : 10.1017/S0140525X12001525 . PMID 23673021 . S2CID 53130527 .
- ^ وانگ، ز. Busemeyer, JR; Atmanspacher، H.; پوتوس، EM (2013). "پتانسیل استفاده از نظریه کوانتومی برای ساخت مدل های شناخت" . مباحث علوم شناختی . 5 (4): 672-688. doi : 10.1111/tops.12043 . PMID 24027215 .
- ↑ Khrennikov، A. (2006). "مغز کوانتومی: "تداخل ذهن"". Biosystems . 84 (3): 225-241. arXiv : quant-ph/0205092 . doi : 10.1016/j.biosystems.2005.11.005 . PMID 16427733 .
- ↑ Khrennikov، A. (2004). پویایی اطلاعات در پدیده های شناختی، روانی، اجتماعی و ناهنجار . نظریه های بنیادی فیزیک. جلد 138. کلوور. شابک 1-4020-1868-1.
- ^ Atmanspacher، H.; رومر، اچ. والاچ، اچ (2002). "نظریه کوانتومی ضعیف: مکمل و درهم تنیدگی در فیزیک و فراتر از آن". مبانی فیزیک . 32 (3): 379-406. doi : 10.1023/A:1014809312397 . S2CID 118583726 .
- ^ آرتس، دی. Aerts, S. (1994). "کاربردهای آمار کوانتومی در مطالعات روانشناختی فرآیندهای تصمیم گیری". مبانی علم . 1 : 85-97. doi : 10.1007/BF00208726 .
- ^ بروزا، پ. کیتو، ک. نلسون، دی. McEvoy, C. (2009). "آیا چیزی شبیه به کوانتومی در واژگان ذهنی انسان وجود دارد؟" . مجله روانشناسی ریاضی . 53 (5): 362-377. doi : 10.1016/j.jmp.2009.04.004 . PMC 2834425 . PMID 20224806 .
- ↑ لامبرت موگیلیانسکی، ا. ضمیر، س. Zwirn، H. (2009). "نامعین بودن نوع: مدلی از KT (Kahneman–Tversky)-man". مجله روانشناسی ریاضی . 53 (5): 349-361. arXiv : فیزیک/0604166 . doi : 10.1016/j.jmp.2009.01.001 . S2CID 15463046 .
- ^پرش به بالا:a b de Barros, JA; ساپس، پی (2009). "مکانیک کوانتومی، تداخل و مغز". مجله روانشناسی ریاضی. 53(5): 306-313. doi:10.1016/j.jmp.2009.03.005.
- ↑ Khrennikov، A. (2008). "مغز کوانتومی در مقیاس های زمانی شناختی و نیمه شناختی". مجله مطالعات آگاهی . 15 (7): 39-77. ISSN 1355-8250 .
- ↑ ون دن نورت، موریتز؛ لیم، سابینا؛ بوش، پگی (26 دسامبر 2016). "در مورد نیاز به یکپارچه سازی علوم اعصاب و فیزیک" . نوروایمونولوژی و التهاب عصبی . 3 (12): 271. doi : 10.20517/2347-8659.2016.55 . hdl : 2066/162618 .
- ↑ Khrennikov، A. (2009). رویکرد متنی به فرمالیسم کوانتومی . نظریه های بنیادی فیزیک. جلد 160. اسپرینگر. شابک 978-1-4020-9592-4.
- ↑ Savage، LJ (1954). مبانی آمار . جان وایلی و پسران
- ^ تورسکی، آ . شفیر، ای (1992). "اثر گسست در انتخاب تحت عدم قطعیت". علم روانشناسی . 3 (5): 305-309. doi : 10.1111/j.1467-9280.1992.tb00678.x . S2CID 144374616 .
- ^ پوتوس، EM; Busemeyer, JR (2009). "توضیح احتمال کوانتومی برای نقض نظریه تصمیم گیری "عقلانی" . مجموعه مقالات انجمن سلطنتی . ب: علوم زیستی. 276 (1665): 2171-2178. doi : 10.1098/rspb.2009.0121 . PMC 2677606 . PMID 19324743 .
- ^پرش به بالا:a b Yukalov, VI; Sornette, D. (21 فوریه 2010). "نظریه تصمیم با تداخل و درهم تنیدگی چشم انداز"(PDF). تئوری و تصمیم. 70(3): 283-328. doi:10.1007/s11238-010-9202-y. hdl: 20.500.11850/29070 . S2CID15377072.
- ↑ موسر، جورج (16 اکتبر 2012). "روشنگری جدید". علمی آمریکایی 307 (5): 76-81. doi : 10.1038/scientificamerican1112-76 .
- ^ آلیس، ام (1953). "Le comportement de l'homme rationnel devant le risque: Critique des postulats et axiomes de l'ecole Americaine". اقتصادسنجی _ 21 (4): 503-546. doi : 10.2307/1907921 . JSTOR 1907921 .
- ^ الزبرگ، دی (1961). "ریسک، ابهام، و بدیهیات وحشی" (PDF) . فصلنامه اقتصاد . 75 (4): 643-669. doi : 10.2307/1884324 . JSTOR 1884324 .
- ^ ماشینا، ام جی (2009). "ریسک، ابهام، و بدیهیات وابستگی رتبه". بررسی اقتصادی آمریکا 99 (1): 385-392. doi : 10.1257/aer.99.1.385 .
- ^ آرتس، دی. سوزو، اس. تاپیا، جی (2012). "یک مدل کوانتومی برای پارادوکس های السبرگ و ماشین". در Busemeyer، J. دوبوا، اف. Lambert-Mogilansky، A. (ویرایشات). تعامل کوانتومی 2012 . LNCS. جلد 7620. برلین: Springer. ص 48-59.
- ^ آرتس، دی. سوزو، اس. تاپیا، جی (2014). "شناسایی ساختارهای کوانتومی در پارادوکس الزبرگ". مجله بین المللی فیزیک نظری . 53 (10): 3666-3682. arXiv : 1302.3850 . Bibcode : 2014IJTP...53.3666A . doi : 10.1007/s10773-014-2086-9 . S2CID 119158347 .
- ^ لا مورا، پی (2009). "فایده مورد انتظار فرافکنی". مجله روانشناسی ریاضی . 53 (5): 408-414. arXiv : 0802.3300 . doi : 10.1016/j.jmp.2009.02.001 . S2CID 12099816 .
- ^ Kak, S. (2017). درختان اطلاعات ناقص و تصمیم گیری کوانتومی کنفرانس بین المللی IEEE در مورد سیستم ها، انسان و سایبرنتیک. بنف، کانادا، اکتبر doi : 10.1109/SMC.2017.8122615 .
- ^ تورسکی، ا. Kahneman، D. (1983). "استدلال بسطی در مقابل شهودی: مغالطه ربط در قضاوت احتمال". بررسی روانشناختی . 90 (4): 293-315. doi : 10.1037/0033-295X.90.4.293 .
- ^ باند، راشل ال. او، یانگ هوی؛ اورمرود، توماس سی (2018). "یک چارچوب کوانتومی برای نسبت های احتمال". مجله بین المللی اطلاعات کوانتومی . 16 (1): 1850002. arXiv : 1508.00936 . Bibcode : 2018IJQI...1650002B . doi : 10.1142/s0219749918500028 . ISSN 0219-7499 . S2CID 85523100 .
- ^پرش به بالا:a b c Aerts, D. (2009). "ساختار کوانتومی در شناخت". مجله روانشناسی ریاضی. 53(5): 314-348. arXiv: 0805.3850 . doi:10.1016/j.jmp.2009.04.005. S2CID14436506.
- ^ Busemeyer, JR; پوتوس، ای. فرانکو، آر. Trueblood، JS (2011). "توضیح نظری کوانتومی برای "خطا" قضاوت احتمال" (PDF) . بررسی روانشناختی . 118 (2): 193–218. doi : 10.1037/a0022542 . PMID 21480739 .
- ^ Trueblood، JS. Busemeyer, JR (2011). "یک حساب احتمال کوانتومی اثرات نظم در استنتاج" . علوم شناختی . 35 (8): 1518-1552. doi : 10.1111/j.1551-6709.2011.01197.x . PMID 21951058 .
- ^ آرتس، دی. بروکارت، جی. اسمتس، اس. (1999). "پارادوکس دروغگو در دیدگاه مکانیک کوانتومی". مبانی علم . 4 (2): 115-132. doi : 10.1023/A:1009610326206 . S2CID 119404170 .
- ^ آرتس، دی. آرتس، اس. بروکارت، جی. گابورا، ال (2000). "نقض نابرابری های بل در جهان کلان". مبانی فیزیک . 30 (9): 1387–1414. arXiv : quant-ph/0007044 . Bibcode : 2000quant.ph..7044A . doi : 10.1023/A:1026449716544 . S2CID 3262876 .
- ^ اوشرسون، DN; اسمیت، EE (1981). "درباره کفایت نظریه نمونه اولیه به عنوان نظریه مفاهیم". شناخت . 9 (1): 35-58. doi : 10.1016/0010-0277(81)90013-5 . PMID 7196818 . S2CID 10482356 .
- ^پرش به بالا:ب همپتون ، JA (1988). "گسترش بیش از حد مفاهیم ربط: شواهدی برای مدل واحدی برای نوعی بودن مفهوم و شمول طبقاتی". مجله روانشناسی تجربی: یادگیری، حافظه و شناخت. 14(1): 12-32. doi:10.1037/0278-7393.14.1.12.
- ^پرش به بالا:ب همپتون ، JA (1988). "تفکیک مفاهیم طبیعی". حافظه و شناخت. 16(6): 579-591. doi: 10.3758/BF03197059 . PMID3193889.
- ^پرش به بالا:a b Aerts، D.; گابورا، ال (2005). "یک مدل حالت-زمینه-ویژگی از مفاهیم و ترکیبات آنها I: ساختار مجموعه های زمینه ها و ویژگی ها". کیبرنتیس_ 34(1و2): 167-191. arXiv: quant-ph/0402207 . doi:10.1108/03684920510575799. S2CID15124657.
- ^پرش به بالا:a b Aerts، D.; گابورا، ال (2005). "یک مدل حالت-زمینه-ویژگی از مفاهیم و ترکیبات آنها II: بازنمایی فضای هیلبرت". کیبرنتیس_ 34(1و2): 192-221. arXiv: quant-ph/0402205 . doi:10.1108/03684920510575807. S2CID13988880.
- ^ گابورا، ال. Aerts، D. (2002). زمینه سازی مفاهیم با استفاده از تعمیم ریاضی فرمالیسم کوانتومی. مجله هوش مصنوعی تجربی و نظری . 14 (4): 327-358. arXiv : quant-ph/0205161 . doi : 10.1080/09528130210162253 . S2CID 10643452 .
- ^پرش به بالا:a b Widdows، D.; پیترز، اس (2003). بردارهای کلمه و منطق کوانتومی: آزمایش هایی با نفی و تفکیک. هشتمین کنفرانس ریاضیات زبان. صص 141-154.
- ^ بروزا، PD; کول، آر جی (2005). "منطق کوانتومی فضای معنایی: بررسی اکتشافی اثرات زمینه در استدلال عملی". در آرتموف، اس . بارینگر، اچ. d'Avila Garcez، AS ; بره، LC; وودز، جی. ما به آنها نشان خواهیم داد: مقالاتی به افتخار Dov Gabbay . انتشارات کالج. شابک 1-904987-11-7.
- ↑ Aerts, D. (2009). "ذرات کوانتومی به عنوان موجودات مفهومی: یک چارچوب توضیحی ممکن برای نظریه کوانتومی". مبانی علم . 14 (4): 361-411. arXiv : 1004.2530 . doi : 10.1007/s10699-009-9166-y . S2CID 119209842 .
- ^ آرتس، دی. بروکارت، جی. گابورا، ال. سوزو، اس (2013). "ساختار کوانتومی و تفکر انسان". علوم رفتاری و مغز . 36 (3): 274-276. doi : 10.1017/S0140525X12002841 . PMID 23673022 .
- ↑ آرتس، دیدریک؛ گابورا، لیان؛ Sozzo, Sandro (سپتامبر 2013). "مفاهیم و پویایی آنها: مدلسازی کوانتومی-نظری از اندیشه انسان". مباحث علوم شناختی . 5 (4): 737-772. arXiv : 1206.1069 . doi : 10.1111/tops.12042 . PMID 24039114 . S2CID 6300002 .
- ^ آرتس، دی. سوزو، اس (2012). "ساختارهای کوانتومی در شناخت: چرا و چگونه مفاهیم در هم تنیده می شوند". در آهنگ، دی. ملوچی، ام. Frommholz، I. (ویرایش.). تعامل کوانتومی 2011 . LNCS. جلد 7052. برلین: Springer. صص 116-127. شابک 978-3-642-24970-9.
- ^ آرتس، دی. سوزو، اس (2014). "درهم تنیدگی کوانتومی در ترکیبات مفهومی". مجله بین المللی فیزیک نظری . 53 (10): 3587-3603. arXiv : 1302.3831 . Bibcode : 2014IJTP...53.3587A . doi : 10.1007/s10773-013-1946-z . S2CID 17064563 .
- ↑ Van Rijsbergen، K. (2004). هندسه بازیابی اطلاعات . انتشارات دانشگاه کمبریج. شابک 0-521-83805-3.
- ↑ Widdows، D. (2006). هندسه و معنا . انتشارات CSLI. شابک 1-57586-448-7.
- ^ آرتس، دی. Czachor، M. (2004). "جنبه های کوانتومی تحلیل معنایی و هوش مصنوعی نمادین". مجله فیزیک الف . 37 (12): L123–L132. arXiv : quant-ph/0309022 . doi : 10.1088/0305-4470/37/12/L01 . S2CID 16701954 .
- ^ سورا، مایکل. "استخراج بدون تجزیه؛ با استفاده از یک ماشین بردار حالت گذرا چند بعدی" (PDF) .
https://en.wikipedia.org/wiki/Quantum_cognition
 . برای مثال، کلاس مفهومی میتواند مجموعه فرمولهای
. برای مثال، کلاس مفهومی میتواند مجموعه فرمولهای  . در مدل PAC (و مدل آگنوستیک مربوطه)، این به طور قابل توجهی تعداد نمونههای مورد نیاز را کاهش نمیدهد: برای هر کلاس مفهومی، پیچیدگی نمونه کلاسیک و کوانتومی تا فاکتورهای ثابت یکسان است.
. در مدل PAC (و مدل آگنوستیک مربوطه)، این به طور قابل توجهی تعداد نمونههای مورد نیاز را کاهش نمیدهد: برای هر کلاس مفهومی، پیچیدگی نمونه کلاسیک و کوانتومی تا فاکتورهای ثابت یکسان است.  و|1〉
و|1〉 در نماد دیراک
در نماد دیراک 
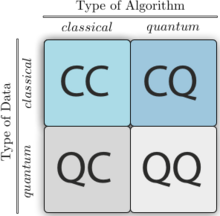
 فعل و انفعالات (سیناپس) یک ماتریس انرژی واقعی و متقارن بر روی شبکه ای از n نورون مصنوعی. کدگذاری به گونهای است که الگوهای مورد نظر حداقلهای محلی انرژی عملکردی هستند و بازیابی با به حداقل رساندن انرژی کل انجام میشود و از یک پیکربندی اولیه شروع میشود.
فعل و انفعالات (سیناپس) یک ماتریس انرژی واقعی و متقارن بر روی شبکه ای از n نورون مصنوعی. کدگذاری به گونهای است که الگوهای مورد نظر حداقلهای محلی انرژی عملکردی هستند و بازیابی با به حداقل رساندن انرژی کل انجام میشود و از یک پیکربندی اولیه شروع میشود. .
. . بنابراین میتوان حافظههای ارتباطی کوانتومی کارآمد و بدون حافظه کاذب را برای هر تعداد چند جملهای از الگوها داشت.
. بنابراین میتوان حافظههای ارتباطی کوانتومی کارآمد و بدون حافظه کاذب را برای هر تعداد چند جملهای از الگوها داشت. کیوبیت توسط2�
کیوبیت توسط2� دامنه های پیچیده، این رمزگذاری اطلاعات می تواند یک نمایش فشرده را به صورت نمایی امکان پذیر کند. به طور شهودی، این مربوط به ارتباط یک توزیع احتمال گسسته بر روی متغیرهای تصادفی باینری با یک بردار کلاسیک است. هدف الگوریتمهای مبتنی بر رمزگذاری دامنه، فرمولبندی الگوریتمهای کوانتومی است که
دامنه های پیچیده، این رمزگذاری اطلاعات می تواند یک نمایش فشرده را به صورت نمایی امکان پذیر کند. به طور شهودی، این مربوط به ارتباط یک توزیع احتمال گسسته بر روی متغیرهای تصادفی باینری با یک بردار کلاسیک است. هدف الگوریتمهای مبتنی بر رمزگذاری دامنه، فرمولبندی الگوریتمهای کوانتومی است که  ، اما آنها به ماتریس های پراکنده محدود نمی شوند.
، اما آنها به ماتریس های پراکنده محدود نمی شوند. در مقایسه با نسخه های کلاسیک k-medias، که در آن�
در مقایسه با نسخه های کلاسیک k-medias، که در آن� تعداد خوشه ها است.
تعداد خوشه ها است. 









 و به طور گسترده مشکوک است کهبسپ⊊بپپ
و به طور گسترده مشکوک است کهبسپ⊊بپپ ، که به طور شهودی به این معنی است که رایانه های کوانتومی از نظر
، که به طور شهودی به این معنی است که رایانه های کوانتومی از نظر 
 ; یعنی تمام مسائلی را که می توان به طور کارآمد با یک کامپیوتر کلاسیک قطعی حل کرد، توسط یک کامپیوتر کوانتومی نیز می تواند به طور کارآمد حل شود، و تمام مسائلی که می توانند به طور موثر توسط یک کامپیوتر کوانتومی حل شوند نیز می توانند توسط یک کامپیوتر کلاسیک قطعی با منابع فضایی چند جمله ای حل شوند. . همچنین گمان می رود که BQP یک ابرمجموعه سخت P است، به این معنی که مشکلاتی وجود دارد که به طور مؤثر توسط رایانه های کوانتومی قابل حل هستند که به طور کارآمدی توسط رایانه های کلاسیک قطعی قابل حل نیستند. برای مثال،
; یعنی تمام مسائلی را که می توان به طور کارآمد با یک کامپیوتر کلاسیک قطعی حل کرد، توسط یک کامپیوتر کوانتومی نیز می تواند به طور کارآمد حل شود، و تمام مسائلی که می توانند به طور موثر توسط یک کامپیوتر کوانتومی حل شوند نیز می توانند توسط یک کامپیوتر کلاسیک قطعی با منابع فضایی چند جمله ای حل شوند. . همچنین گمان می رود که BQP یک ابرمجموعه سخت P است، به این معنی که مشکلاتی وجود دارد که به طور مؤثر توسط رایانه های کوانتومی قابل حل هستند که به طور کارآمدی توسط رایانه های کلاسیک قطعی قابل حل نیستند. برای مثال،  ; یعنی اعتقاد بر این است که مسائلی وجود دارد که به طور موثر قابل بررسی هستند که به طور کارآمدی توسط یک کامپیوتر کوانتومی قابل حل نیستند. به عنوان پیامد مستقیم این باور، همچنین گمان می رود که BQP از کلاس مسائل
; یعنی اعتقاد بر این است که مسائلی وجود دارد که به طور موثر قابل بررسی هستند که به طور کارآمدی توسط یک کامپیوتر کوانتومی قابل حل نیستند. به عنوان پیامد مستقیم این باور، همچنین گمان می رود که BQP از کلاس مسائل 
 بر فراز
بر فراز پرس و جو به پایگاه داده، درجه دوم کمتر از
پرس و جو به پایگاه داده، درجه دوم کمتر از پرس و جوهای مورد نیاز برای الگوریتم های کلاسیک در این مورد، مزیت نه تنها قابل اثبات است، بلکه بهینه است: نشان داده شده است که الگوریتم گروور حداکثر احتمال ممکن را برای یافتن عنصر مورد نظر برای هر تعداد جستجوی اوراکل می دهد. نمونههای زیادی از سرعتهای کوانتومی قابل اثبات برای مسائل پرس و جو بر اساس الگوریتم گروور است، از جمله
پرس و جوهای مورد نیاز برای الگوریتم های کلاسیک در این مورد، مزیت نه تنها قابل اثبات است، بلکه بهینه است: نشان داده شده است که الگوریتم گروور حداکثر احتمال ممکن را برای یافتن عنصر مورد نظر برای هر تعداد جستجوی اوراکل می دهد. نمونههای زیادی از سرعتهای کوانتومی قابل اثبات برای مسائل پرس و جو بر اساس الگوریتم گروور است، از جمله 


 نقطه ای در سطح کره است، در قسمتی بین قطب ها،
نقطه ای در سطح کره است، در قسمتی بین قطب ها،
 و جرمم
و جرمم در میدان الکتریکی ac رفتار می کند
در میدان الکتریکی ac رفتار می کند . نیروی وارد بر یون توسط
. نیروی وارد بر یون توسط ، بنابراین با
، بنابراین با  .
. ،
، ،
، ثابت یکپارچگی است. بنابراین، یون با فرکانس زاویه ای نوسان می کند
ثابت یکپارچگی است. بنابراین، یون با فرکانس زاویه ای نوسان می کند و دامنه متناسب با شدت میدان الکتریکی. یک پتانسیل به دام انداختن را می توان با تغییر فضایی قدرت میدان الکتریکی ac به دست آورد.
و دامنه متناسب با شدت میدان الکتریکی. یک پتانسیل به دام انداختن را می توان با تغییر فضایی قدرت میدان الکتریکی ac به دست آورد. -محور واقع در گوشه های یک مربع در
-محور واقع در گوشه های یک مربع در -سطح. الکترودها به صورت مورب در مقابل یکدیگر وصل شده اند و یک ولتاژ ac
-سطح. الکترودها به صورت مورب در مقابل یکدیگر وصل شده اند و یک ولتاژ ac اعمال می شود. در طول
اعمال می شود. در طول .
. و
و توسط شرایط مرزی روی الکترودها و
توسط شرایط مرزی روی الکترودها و معادله
معادله  . با فرض طول الکترودها
. با فرض طول الکترودها بسیار بیشتر از جدایی آنها است
بسیار بیشتر از جدایی آنها است ، می توان نشان داد که
، می توان نشان داد که .
. .
. ، معادلات حرکت در
، معادلات حرکت در .
.
 .
. ، نیروی
، نیروی  -محور. برای میدان مغناطیسی یکنواخت
-محور. برای میدان مغناطیسی یکنواخت ، نیروی
، نیروی  .
. ،
، ،
، .
. و سرعت رانش در
و سرعت رانش در -جهت. سرعت رانش عمود بر جهت میدان الکتریکی است.
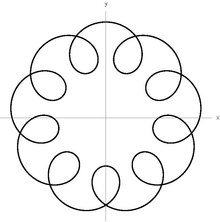
-جهت. سرعت رانش عمود بر جهت میدان الکتریکی است. ، فرکانس مگنترون نامیده می شود. یک یون دارای فرکانس مشخصه سوم نیز خواهد بود
، فرکانس مگنترون نامیده می شود. یک یون دارای فرکانس مشخصه سوم نیز خواهد بود بین دو الکترود کلاهک انتهایی فرکانس ها معمولاً مقادیر بسیار متفاوتی دارند
بین دو الکترود کلاهک انتهایی فرکانس ها معمولاً مقادیر بسیار متفاوتی دارند .
. 




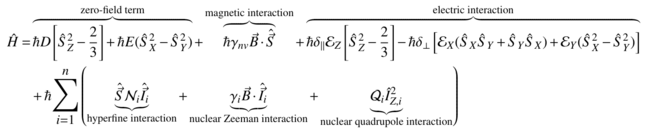

 عملیات ماتریس واحد ((ن)
عملیات ماتریس واحد ((ن) ) را می توان تنها با استفاده از آینه ها، تقسیم کننده های پرتو و شیفترهای فاز
) را می توان تنها با استفاده از آینه ها، تقسیم کننده های پرتو و شیفترهای فاز  ورودی ها ون
ورودی ها ون عناصر نوری خطی بر اساس دلیل جهانی بودن و پیچیدگی، LOQC معمولاً فقط از آینهها، تقسیمکنندههای پرتو، شیفترهای فاز و ترکیبات آنها مانند
عناصر نوری خطی بر اساس دلیل جهانی بودن و پیچیدگی، LOQC معمولاً فقط از آینهها، تقسیمکنندههای پرتو، شیفترهای فاز و ترکیبات آنها مانند  ،
، یک
یک  ، احتمال دارد||2
، احتمال دارد||2 از بودن در
از بودن در از بودن در|1〉
از بودن در|1〉 شرایط عادی سازی است. حالت نوری یک کانال ارتباطی نوری قابل تشخیص است که معمولاً توسط زیرنویس های یک حالت کوانتومی برچسب گذاری می شود. راه های زیادی برای تعریف کانال های ارتباطی نوری قابل تشخیص وجود دارد. به عنوان مثال، مجموعه ای از حالت ها می تواند
شرایط عادی سازی است. حالت نوری یک کانال ارتباطی نوری قابل تشخیص است که معمولاً توسط زیرنویس های یک حالت کوانتومی برچسب گذاری می شود. راه های زیادی برای تعریف کانال های ارتباطی نوری قابل تشخیص وجود دارد. به عنوان مثال، مجموعه ای از حالت ها می تواند  و
و . مرسوم است که به حالت هایی که از طریق اشغال حالت ها به عنوان حالت های
. مرسوم است که به حالت هایی که از طریق اشغال حالت ها به عنوان حالت های  سیستم کوانتومی سطح).
سیستم کوانتومی سطح). (زیرنویس ها برای این مورد تک کیوبیت نادیده گرفته می شوند). با استفاده از یک منبع تک فوتون شرطی، وضعیت خروجی تضمین می شود، اگرچه ممکن است چندین تلاش (بسته به میزان موفقیت) نیاز داشته باشد. یک حالت چند کیوبیتی مشترک را می توان به روشی مشابه تهیه کرد. به طور کلی، یک حالت کوانتومی دلخواه می تواند برای QIP با مجموعه ای مناسب از منابع فوتون ایجاد شود.
(زیرنویس ها برای این مورد تک کیوبیت نادیده گرفته می شوند). با استفاده از یک منبع تک فوتون شرطی، وضعیت خروجی تضمین می شود، اگرچه ممکن است چندین تلاش (بسته به میزان موفقیت) نیاز داشته باشد. یک حالت چند کیوبیتی مشترک را می توان به روشی مشابه تهیه کرد. به طور کلی، یک حالت کوانتومی دلخواه می تواند برای QIP با مجموعه ای مناسب از منابع فوتون ایجاد شود. است:
است: ،
، و
و تحت شرایط تبدیل
تحت شرایط تبدیل 
 ، می توان آن را نشان داد
، می توان آن را نشان داد ،
، در
در  .
. .
. با یک اپراتور واحد که توسط
با یک اپراتور واحد که توسط ، یا اگر در قالب 2 حالته نوشته شده باشد
، یا اگر در قالب 2 حالته نوشته شده باشد ،
، درباره
درباره
 ).
).

 نشان دهنده یک
نشان دهنده یک  نشان دهنده یک فوتون در حالت پایین است.
نشان دهنده یک فوتون در حالت پایین است.
 تعداد حالت ها است) و همه حالت های دیگر خالی هستند.
تعداد حالت ها است) و همه حالت های دیگر خالی هستند.




![{\displaystyle O({\sqrt[{3}]{N}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a953364313112d7f3243feb0c59146295a65263d)
 ، ممکن است اجازه دهد حتی کامپیوترهای سریع تری ساخته شوند. با این حال، تعریف محاسبات در این نظریه ها به دلیل
، ممکن است اجازه دهد حتی کامپیوترهای سریع تری ساخته شوند. با این حال، تعریف محاسبات در این نظریه ها به دلیل 


 زمان
زمان  زمان و بهترین حد بالا برای پیچیدگی این مشکل است
زمان و بهترین حد بالا برای پیچیدگی این مشکل است .
.  برای سیستمی با n
برای سیستمی با n  ، که در آن داده ها در یک ثبات کوانتومی ذخیره می شود توسط داده می شود
، که در آن داده ها در یک ثبات کوانتومی ذخیره می شود توسط داده می شود جایی که
جایی که ضرب
ضرب  ، در حالی که
، در حالی که  )، و غیره. برای ثباتی متشکل از N تعداد سیستمهای کوانتومی d بعدی (یا سطح d ) فضای هیلبرت داریم.
)، و غیره. برای ثباتی متشکل از N تعداد سیستمهای کوانتومی d بعدی (یا سطح d ) فضای هیلبرت داریم.
 ارزش ها
ارزش ها
 بنابراین
بنابراین 


 بر این اساس.
بر این اساس. و
و ، با استفاده از تعریف ثبت کوانتومی
، با استفاده از تعریف ثبت کوانتومی نتیجه می شود که قادر است تمام مقادیر ممکن را (با داشتن دامنه احتمال غیر صفر برای همه نتایج) که توسط دو کیوبیت به طور همزمان در بر می گیرد، ذخیره کند.
نتیجه می شود که قادر است تمام مقادیر ممکن را (با داشتن دامنه احتمال غیر صفر برای همه نتایج) که توسط دو کیوبیت به طور همزمان در بر می گیرد، ذخیره کند.

 .
.












 به این معنی است که تابع یک تابع
به این معنی است که تابع یک تابع 






 برای
برای . حالت سنتی GHZ برای آن تعریف شد
. حالت سنتی GHZ برای آن تعریف شد . حالت های GHZ گهگاه به
. حالت های GHZ گهگاه به 
 به جز کت های پایه 0 و 1 با " فوتون های N در یک حالت هستند " و " فوتون های N در حالت دیگر هستند " جایگزین شده اند.
به جز کت های پایه 0 و 1 با " فوتون های N در یک حالت هستند " و " فوتون های N در حالت دیگر هستند " جایگزین شده اند.

 حالت های گاوسی حالت ( برای یک رویکرد به ظاهر متفاوت اما اساساً معادل به رفر.
حالت های گاوسی حالت ( برای یک رویکرد به ظاهر متفاوت اما اساساً معادل به رفر.  حالت های گاوسی، اما دیگر برای آن کافی نیست
حالت های گاوسی، اما دیگر برای آن کافی نیست حالت های گاوسی. شرایط سیمون را می توان با در نظر گرفتن ممان های مرتبه بالاتر عملگرهای متعارف
حالت های گاوسی. شرایط سیمون را می توان با در نظر گرفتن ممان های مرتبه بالاتر عملگرهای متعارف 
 ، به صورت زیر:
، به صورت زیر: 

 ،
،  . سپس آنتروپی شانون به صورت زیر است:
. سپس آنتروپی شانون به صورت زیر است: .
.






 .
.
 و
و اپراتور هویت در
اپراتور هویت در .
. 

 مورد بحث در بالا است
مورد بحث در بالا است .
. و
و در همان کلاس SLOCC به همان اندازه قدرتمند هستند (از آنجایی که می توانم یکی را به دیگری تبدیل کنم و سپس هر کاری که به من اجازه می دهد انجام دهم)، اما از آنجایی که تبدیل ها
در همان کلاس SLOCC به همان اندازه قدرتمند هستند (از آنجایی که می توانم یکی را به دیگری تبدیل کنم و سپس هر کاری که به من اجازه می دهد انجام دهم)، اما از آنجایی که تبدیل ها و
و ممکن است با احتمال متفاوت موفق شوند، دیگر به یک اندازه ارزشمند نیستند. به عنوان مثال، برای دو کیوبیت خالص تنها دو کلاس SLOCC وجود دارد: حالتهای درهمتنیده (که شامل حالات بل (بیشترین درهمتنیده) است و حالتهای درهمتنیده ضعیف مانند
ممکن است با احتمال متفاوت موفق شوند، دیگر به یک اندازه ارزشمند نیستند. به عنوان مثال، برای دو کیوبیت خالص تنها دو کلاس SLOCC وجود دارد: حالتهای درهمتنیده (که شامل حالات بل (بیشترین درهمتنیده) است و حالتهای درهمتنیده ضعیف مانند ) و آنهایی که قابل تفکیک هستند (یعنی حالتهای محصول مانند
) و آنهایی که قابل تفکیک هستند (یعنی حالتهای محصول مانند ).
).  ممکن است. یک طبقه بندی بسیار مهم (و بسیار درشت) بر اساس این ویژگی است که آیا می توان تعداد زیادی کپی از یک حالت را به طور دلخواه تغییر داد.
ممکن است. یک طبقه بندی بسیار مهم (و بسیار درشت) بر اساس این ویژگی است که آیا می توان تعداد زیادی کپی از یک حالت را به طور دلخواه تغییر داد. حداقل به یک حالت درهم تنیده خالص. کشورهایی که این خاصیت را دارند قابل
حداقل به یک حالت درهم تنیده خالص. کشورهایی که این خاصیت را دارند قابل  ، اما همیشه می توان با استفاده از متغیرهای پنهان محلی توصیف کرد.
، اما همیشه می توان با استفاده از متغیرهای پنهان محلی توصیف کرد. 
 و دومی در حالت
و دومی در حالت ، وضعیت سیستم ترکیبی است
، وضعیت سیستم ترکیبی است
 برای
برای  برای
برای  .
.![{\displaystyle [c_{i}^{A}]،[c_{j}^{B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2b47f980dac5bc92f73609aef7a6280f2f2be7f) به طوری که
به طوری که تسلیم شدن
تسلیم شدن و
و اگر برای هر بردار، جدایی ناپذیر است
اگر برای هر بردار، جدایی ناپذیر است ما داریم
ما داریم اگر حالتی غیرقابل تفکیک باشد، به آن «حالت درهم تنیده» می گویند.
اگر حالتی غیرقابل تفکیک باشد، به آن «حالت درهم تنیده» می گویند. از
از  از
از 
 .
. .
.
 . هنگامی که یک حالت مختلط دارای رتبه 1 است، بنابراین یک "گروه خالص" را توصیف می کند. هنگامی که اطلاعات کمتر از کل در مورد وضعیت یک سیستم کوانتومی وجود دارد، ما به
. هنگامی که یک حالت مختلط دارای رتبه 1 است، بنابراین یک "گروه خالص" را توصیف می کند. هنگامی که اطلاعات کمتر از کل در مورد وضعیت یک سیستم کوانتومی وجود دارد، ما به  با
با 
![{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\ بتا _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf2f7c56adc4e273d3e3c73ee6a66e190c3f35c)
 و بردارها بردار واحد هستند. این خود ملحق و مثبت است و رد 1 دارد.
و بردارها بردار واحد هستند. این خود ملحق و مثبت است و رد 1 دارد.
 'شن
'شن 'ها خود حالت های مختلط (عملگرهای چگالی) در زیر سیستم های
'ها خود حالت های مختلط (عملگرهای چگالی) در زیر سیستم های 
