1-یادگیری ماشین کوانتومی

از ویکیپدیا، دانشنامه آزاد

به نظر می رسد یکی از مشارکت کنندگان اصلی این مقاله ارتباط نزدیکی با موضوع آن داشته باشد. ممکن است برای مطابقت با خط‌مشی‌های محتوای ویکی‌پدیا، به‌ویژه دیدگاه خنثی ، نیاز به پاک‌سازی داشته باشد . لطفاً در صفحه بحث بیشتر بحث کنید . ( سپتامبر 2018 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

این مقاله ممکن است نیاز به بازنویسی داشته باشد تا با استانداردهای کیفیت ویکی‌پدیا مطابقت داشته باشد . شما می توانید کمک کنید . شاید صفحه گفتگو شامل پیشنهاداتی باشد. ( ژوئیه 2023 )

مکانیک کوانتومی
بخشی از مجموعه مقالات در مورد
منℏ∂∂تی\|�(تی)〉=اچ^\|�(تی)〉 $i\hbar {\frac {\partial }{\partial t}}\|\psi (t)\rangle ={\hat {H}}\|\psi (t)\rangle$ معادله شرودینگر
معرفی واژه نامه تاریخ
نشان می دهد زمینه
نشان می دهد مبانی
نشان می دهد آزمایش
نشان می دهد فرمولاسیون
نشان می دهد معادلات
نشان می دهد تفاسیر
نشان می دهد موضوعات پیشرفته
نشان می دهد دانشمندان
v تی ه

یادگیری ماشین کوانتومی ادغام الگوریتم های کوانتومی در برنامه های یادگیری ماشین است . [1] [2] [3] [4] [5] [6] [7] [8]

رایج ترین استفاده از این اصطلاح به الگوریتم های یادگیری ماشین برای تجزیه و تحلیل داده های کلاسیک اجرا شده بر روی یک کامپیوتر کوانتومی اشاره دارد ، یعنی یادگیری ماشین با کوانتومی پیشرفته. [9] [10] [11] در حالی که الگوریتم‌های یادگیری ماشین برای محاسبه مقادیر بسیار زیاد داده استفاده می‌شوند، یادگیری ماشین کوانتومی از کیوبیت‌ها و عملیات کوانتومی یا سیستم‌های کوانتومی تخصصی برای بهبود سرعت محاسباتی و ذخیره داده‌ها توسط الگوریتم‌ها در یک برنامه استفاده می‌کند. [12] این شامل روش‌های ترکیبی می‌شود که شامل پردازش کلاسیک و کوانتومی می‌شود، جایی که برنامه‌های فرعی سخت محاسباتی به یک دستگاه کوانتومی برون‌سپاری می‌شوند. [13] [14] [15] این روال‌ها می‌توانند ماهیت پیچیده‌تری داشته باشند و در یک کامپیوتر کوانتومی سریع‌تر اجرا شوند. [7] علاوه بر این، الگوریتم‌های کوانتومی را می‌توان برای تحلیل حالت‌های کوانتومی به جای داده‌های کلاسیک استفاده کرد. [16] [17]

فراتر از محاسبات کوانتومی، اصطلاح «یادگیری ماشین کوانتومی» با روش‌های یادگیری ماشین کلاسیک نیز مرتبط است که برای داده‌های تولید شده از آزمایش‌های کوانتومی (یعنی یادگیری ماشینی سیستم‌های کوانتومی )، مانند یادگیری انتقال فاز یک سیستم کوانتومی استفاده می‌شود [18] [19 ]. ] یا ایجاد آزمایش های کوانتومی جدید. [20] [21] [22]

یادگیری ماشین کوانتومی همچنین به شاخه ای از تحقیقات گسترش می یابد که شباهت های روش شناختی و ساختاری بین سیستم های فیزیکی خاص و سیستم های یادگیری، به ویژه شبکه های عصبی را بررسی می کند. به عنوان مثال، برخی از تکنیک های ریاضی و عددی از فیزیک کوانتومی برای یادگیری عمیق کلاسیک و بالعکس قابل استفاده هستند. [23] [24] [25]

علاوه بر این، محققان مفاهیم انتزاعی بیشتری از نظریه یادگیری را با توجه به اطلاعات کوانتومی، که گاهی اوقات به عنوان "نظریه یادگیری کوانتومی" نامیده می شود، بررسی می کنند. [26] [27]

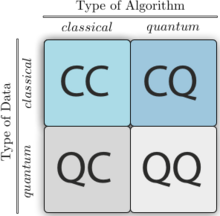
چهار رویکرد مختلف برای ترکیب رشته‌های محاسبات کوانتومی و یادگیری ماشین. [28] [29] حرف اول به کلاسیک یا کوانتومی بودن سیستم مورد مطالعه اشاره دارد، در حالی که حرف دوم مشخص می کند که آیا یک دستگاه پردازش اطلاعات کلاسیک یا کوانتومی استفاده می شود.

یادگیری ماشین با کامپیوترهای کوانتومی [ ویرایش ]

یادگیری ماشینی پیشرفته کوانتومی به الگوریتم‌های کوانتومی اشاره دارد که وظایف را در یادگیری ماشین حل می‌کند و در نتیجه تکنیک‌های یادگیری ماشین کلاسیک را بهبود می‌بخشد و اغلب تسریع می‌کند. چنین الگوریتم‌هایی معمولاً نیازمند کدگذاری مجموعه داده‌های کلاسیک در یک کامپیوتر کوانتومی هستند تا برای پردازش اطلاعات کوانتومی قابل دسترسی باشد. متعاقباً، روال‌های پردازش اطلاعات کوانتومی اعمال می‌شوند و نتیجه محاسبات کوانتومی با اندازه‌گیری سیستم کوانتومی خوانده می‌شود. به عنوان مثال، نتیجه اندازه گیری یک کیوبیت، نتیجه یک کار طبقه بندی باینری را نشان می دهد. در حالی که بسیاری از پیشنهادات الگوریتم‌های یادگیری ماشین کوانتومی هنوز کاملاً تئوری هستند و برای آزمایش به یک کامپیوتر کوانتومی جهانی در مقیاس کامل نیاز دارند ، برخی دیگر بر روی دستگاه‌های کوانتومی در مقیاس کوچک یا با هدف خاص پیاده‌سازی شده‌اند.

حافظه های انجمنی کوانتومی و تشخیص الگوی کوانتومی [ ویرایش ]

انجمنی (یا خاطرات آدرس‌پذیر محتوا) می‌توانند محتوای ذخیره‌شده را بر اساس معیار تشابه تشخیص دهند، نه آدرس‌های ثابت، مانند حافظه‌های دسترسی تصادفی. به این ترتیب، آنها باید بتوانند الگوهای ناقص و خراب را بازیابی کنند، وظیفه اصلی یادگیری ماشین در تشخیص الگو.

حافظه های انجمنی کلاسیک معمولی الگوهای p را در حافظه ذخیره می کنند�(�2) $O(n^{2})$ فعل و انفعالات (سیناپس) یک ماتریس انرژی واقعی و متقارن بر روی شبکه ای از n نورون مصنوعی. کدگذاری به گونه‌ای است که الگوهای مورد نظر حداقل‌های محلی انرژی عملکردی هستند و بازیابی با به حداقل رساندن انرژی کل انجام می‌شود و از یک پیکربندی اولیه شروع می‌شود.

متأسفانه، خاطرات تداعی کلاسیک به شدت توسط پدیده گفتگوی متقابل محدود شده است. هنگامی که الگوهای زیادی ذخیره می شوند، خاطرات جعلی ظاهر می شوند که به سرعت تکثیر می شوند، به طوری که چشم انداز انرژی نامنظم می شود و دیگر امکان بازیابی وجود ندارد. تعداد الگوهای قابل ذخیره معمولاً توسط یک تابع خطی از تعداد نورون ها محدود می شود.پ≤�(�) $p\leq O(n)$ .

خاطرات تداعی کوانتومی [2] [3] [4] (در ساده ترین شکل ممکن) الگوها را در یک ماتریس واحد U ذخیره می کند که بر روی فضای هیلبرت n کیوبیتی عمل می کند. بازیابی با تکامل واحد از یک حالت اولیه ثابت به یک برهم نهی کوانتومی از الگوهای مورد نظر با توزیع احتمال به اوج خود در شبیه ترین الگوی به ورودی تحقق می یابد. بنابراین، فرآیند بازیابی به دلیل ماهیت کوانتومی خود احتمالی است. از آنجایی که حافظه‌های تداعی کوانتومی عاری از گفتگو هستند، حافظه‌های جعلی هرگز تولید نمی‌شوند. به همین ترتیب، آنها ظرفیت برتری نسبت به کلاسیک دارند. تعداد پارامترهای ماتریس واحد U است�(پ�) $O(pn)$ . بنابراین می‌توان حافظه‌های ارتباطی کوانتومی کارآمد و بدون حافظه کاذب را برای هر تعداد چند جمله‌ای از الگوها داشت.

شبیه سازی جبر خطی با دامنه های کوانتومی [ ویرایش ]

تعدادی از الگوریتم‌های کوانتومی برای یادگیری ماشین مبتنی بر ایده رمزگذاری دامنه هستند، یعنی ارتباط دادن دامنه‌های یک حالت کوانتومی با ورودی‌ها و خروجی‌های محاسبات. [30] [31] [32] از آنجایی که یک حالت� $n$ کیوبیت توسط2� $2^{n}$ دامنه های پیچیده، این رمزگذاری اطلاعات می تواند یک نمایش فشرده را به صورت نمایی امکان پذیر کند. به طور شهودی، این مربوط به ارتباط یک توزیع احتمال گسسته بر روی متغیرهای تصادفی باینری با یک بردار کلاسیک است. هدف الگوریتم‌های مبتنی بر رمزگذاری دامنه، فرمول‌بندی الگوریتم‌های کوانتومی است که منابع آنها به صورت چندجمله‌ای در تعداد کیوبیت‌ها رشد می‌کنند.� $n$ ، که به پیچیدگی زمانی لگاریتمی در تعداد دامنه ها و در نتیجه بعد ورودی می رسد.

بسیاری از الگوریتم‌های یادگیری ماشین کوانتومی در این دسته بر اساس تغییرات الگوریتم کوانتومی برای سیستم‌های معادلات خطی [33] (به‌عنوان محاوره‌ای HHL، به نام نویسندگان مقاله) که تحت شرایط خاص، وارونگی ماتریس را با استفاده از مقداری منابع فیزیکی انجام می‌دهند، هستند. تنها به صورت لگاریتمی در ابعاد ماتریس رشد می کند. یکی از این شرایط این است که یک همیلتونی که از نظر ورودی با ماتریس مطابقت دارد، می تواند به طور موثر شبیه سازی شود، که اگر ماتریس پراکنده باشد [34] یا رتبه پایین، ممکن است. [35] برای مرجع، هر الگوریتم کلاسیک شناخته شده برای وارونگی ماتریس به تعدادی عملیات نیاز دارد که بیش از درجه دوم در بعد ماتریس رشد می کند (مثلا�(�2.373) $O{\mathord {\left(n^{2.373}\right)}}$ ، اما آنها به ماتریس های پراکنده محدود نمی شوند.

وارونگی ماتریس کوانتومی را می توان برای روش های یادگیری ماشین اعمال کرد که در آن آموزش به حل یک سیستم خطی معادلات کاهش می یابد ، به عنوان مثال در رگرسیون خطی حداقل مربعات، [31] [32] نسخه حداقل مربعات ماشین های بردار پشتیبان ، [30] ] و فرآیندهای گاوسی. [36]

یکی از گلوگاه‌های مهم روش‌هایی که محاسبات جبر خطی را با دامنه‌های حالت‌های کوانتومی شبیه‌سازی می‌کنند، آماده‌سازی حالت است، که اغلب نیاز به مقداردهی اولیه یک سیستم کوانتومی در حالتی دارد که دامنه‌های آن منعکس‌کننده ویژگی‌های کل مجموعه داده است. اگرچه روش های کارآمد برای آماده سازی حالت برای موارد خاص شناخته شده است، [37] [38] این مرحله به راحتی پیچیدگی کار را پنهان می کند. [39] [40]

الگوریتم های کوانتومی متغیر (VQAs) [ ویرایش ]

VQAها یکی از الگوریتم‌های کوانتومی هستند که بیشتر مورد مطالعه قرار گرفته‌اند، زیرا محققان انتظار دارند که تمام برنامه‌های کاربردی مورد نیاز برای رایانه‌های کوانتومی از VQAها استفاده کنند و همچنین به نظر می‌رسد که VQAها انتظارات برای کسب برتری کوانتومی را برآورده می‌کنند. VQAs یک رویکرد ترکیبی کوانتومی-کلاسیک است که در آن پردازنده کوانتومی حالت‌های کوانتومی را آماده می‌کند و اندازه‌گیری انجام می‌شود و بهینه‌سازی توسط یک کامپیوتر کلاسیک انجام می‌شود. VQA ها برای NISQ بهترین در نظر گرفته می شوند زیرا VQA ها نسبت به سایر الگوریتم ها نسبت به سایر الگوریتم ها مقاوم به نویز هستند و تنها با چند صد کیوبیت برتری کوانتومی را به ارمغان می آورند. محققان الگوریتم‌های مبتنی بر مدار را برای حل مسائل بهینه‌سازی و یافتن انرژی حالت پایه سیستم‌های پیچیده مورد مطالعه قرار داده‌اند، که حل آن‌ها دشوار بود یا برای انجام محاسبات با استفاده از رایانه کلاسیک به زمان زیادی نیاز داشت. [41] [42]

مدارهای کوانتومی متغیر (VQCs) [ ویرایش ]

مدارهای کوانتومی متغیر که به عنوان مدارهای کوانتومی پارامتریزه شده (PQC) نیز شناخته می شوند، بر اساس الگوریتم های کوانتومی متغیر (VQA) هستند. VQC ها از سه بخش، آماده سازی حالت های اولیه، مدار کوانتومی و اندازه گیری تشکیل شده اند. محققان به طور گسترده در حال مطالعه VQC ها هستند، زیرا از قدرت محاسبات کوانتومی برای یادگیری در زمان کوتاه استفاده می کند و همچنین از پارامترهای کمتری نسبت به همتایان کلاسیک خود استفاده می کند. از نظر تئوری و عددی ثابت شده است که می‌توانیم توابع غیرخطی، مانند توابع مورد استفاده در شبکه‌های عصبی، در مدارهای کوانتومی را تقریب بزنیم. به دلیل برتری VQCها، شبکه عصبی با VQCها در وظایف یادگیری تقویتی و الگوریتم های مولد جایگزین شده است. ماهیت ذاتی دستگاه‌های کوانتومی نسبت به عدم پیوستگی، خطای دروازه تصادفی و خطاهای اندازه‌گیری باعث شده است که پتانسیل بالایی برای محدود کردن آموزش مدارهای تغییرات داشته باشند. آموزش VQC ها بر روی دستگاه های کلاسیک قبل از استفاده از آنها در دستگاه های کوانتومی به غلبه بر مشکل نویز ناهمدوسی که از طریق تعداد تکرارها برای آموزش ایجاد می شود، کمک می کند. [43] [44] [45]

طبقه بندی کننده باینری کوانتومی [ ویرایش ]

سازماندهی مجدد الگو یکی از وظایف مهم یادگیری ماشینی است، طبقه بندی باینری یکی از ابزارها یا الگوریتم های یافتن الگوها است. طبقه بندی باینری در یادگیری نظارت شده و در یادگیری بدون نظارت استفاده می شود . در یادگیری ماشین کوانتومی، بیت‌های کلاسیک به کیوبیت تبدیل می‌شوند و به فضای هیلبرت نگاشت می‌شوند. برای استفاده از مزیت فضای هیلبرت، از داده‌های مقادیر پیچیده در طبقه‌بندی‌کننده باینری کوانتومی استفاده می‌شود. [46] [47] با بهره‌برداری از ویژگی‌های مکانیک کوانتومی مانند برهم‌نهی، درهم‌تنیدگی، تداخل، طبقه‌بندی‌کننده دوتایی کوانتومی نتیجه دقیق را در مدت زمان کوتاهی تولید می‌کند. [48]

الگوریتم های یادگیری ماشین کوانتومی بر اساس جستجوی گروور [ ویرایش ]

روش دیگری برای بهبود یادگیری ماشین کلاسیک با پردازش اطلاعات کوانتومی از روش‌های تقویت دامنه مبتنی بر الگوریتم جستجوی گروور استفاده می‌کند که نشان داده شده است که مشکلات جستجوی بدون ساختار را با سرعت دوم در مقایسه با الگوریتم‌های کلاسیک حل می‌کند. این روال‌های کوانتومی را می‌توان برای الگوریتم‌های یادگیری که به یک کار جستجوی ساختاریافته تبدیل می‌شوند، به کار برد، همانطور که می‌توان برای مثال در مورد k -medias [49] و الگوریتم‌های k-نزدیک‌ترین همسایه‌ها انجام داد . [9] کاربرد دیگر افزایش سرعت درجه دوم در آموزش پرسپترون است . [50]

نمونه ای از تقویت دامنه که در الگوریتم یادگیری ماشین استفاده می شود، کمینه سازی الگوریتم جستجوی گروور است. که در آن یک زیربرنامه از الگوریتم جستجوی گروور برای یافتن عنصری کمتر از برخی از عناصر تعریف شده قبلی استفاده می کند. این را می توان با یک اوراکل انجام داد که تعیین می کند آیا یک حالت با عنصر مربوطه کمتر از حالت از پیش تعریف شده است یا خیر. سپس الگوریتم گروور می تواند عنصری را پیدا کند که شرط ما برآورده شود. کمینه سازی توسط برخی از عناصر تصادفی در مجموعه داده ما مقداردهی اولیه می شود و به طور مکرر این زیر روال را برای یافتن حداقل عنصر در مجموعه داده انجام می دهد. این کمینه سازی به طور قابل توجهی در میانه های k کوانتومی استفاده می شود و حداقل سرعت آن افزایش می یابد�(�/ک) $O({\sqrt {n/k}})$ در مقایسه با نسخه های کلاسیک k-medias، که در آن� $n$ تعداد نقاط داده وک $k$ تعداد خوشه ها است. [49]

تقویت دامنه اغلب با راه رفتن کوانتومی ترکیب می شود تا به همان سرعت درجه دوم برسد. پیاده‌روی‌های کوانتومی برای بهبود الگوریتم رتبه صفحه گوگل [51] و همچنین عملکرد عوامل یادگیری تقویتی در چارچوب شبیه‌سازی تصویری پیشنهاد شده‌اند. [52]

یادگیری تقویتی کوانتومی [ ویرایش ]

یادگیری تقویتی شاخه ای از یادگیری ماشینی است که از یادگیری تحت نظارت و بدون نظارت متمایز است، که پیشرفت های کوانتومی را نیز می پذیرد. [53] [52] [54] در یادگیری تقویت شده کوانتومی، یک عامل کوانتومی با یک محیط کلاسیک یا کوانتومی در تعامل است و گهگاه برای اعمال خود پاداش دریافت می کند، که به عامل اجازه می دهد رفتار خود را تطبیق دهد - به عبارت دیگر، یاد بگیرد که چه چیزی انجام دهید تا پاداش بیشتری کسب کنید. در برخی شرایط، یا به دلیل قابلیت پردازش کوانتومی عامل، [52] یا به دلیل امکان بررسی محیط در برهم نهی ها ، [29] ممکن است یک سرعت کوانتومی حاصل شود. پیاده سازی این نوع پروتکل ها برای سیستم های یون های به دام افتاده [55] و مدارهای ابررسانا پیشنهاد شده است . [56] سرعت کوانتومی زمان تصمیم گیری داخلی عامل [52] به طور تجربی در یون های به دام افتاده نشان داده شده است، [57] در حالی که سرعت کوانتومی زمان یادگیری در یک برهمکنش کاملا منسجم (کوانتومی) بین عامل و محیط به طور تجربی در یک تنظیم فوتونیک تحقق یافته است. [58]

آنیل کوانتومی [ ویرایش ]

مقاله اصلی: آنیل کوانتومی

بازپخت کوانتومی یک تکنیک بهینه‌سازی است که برای تعیین مینیمم و ماکزیمم محلی یک تابع در مجموعه معینی از توابع کاندید استفاده می‌شود. این روشی برای گسسته کردن یک تابع با مینیمم ها یا ماکزیمم های محلی فراوان به منظور تعیین قابل مشاهده های تابع است. این فرآیند را می توان از بازپخت شبیه سازی شده توسط فرآیند تونل زنی کوانتومی متمایز کرد ، که توسط آن ذرات از طریق موانع جنبشی یا بالقوه از حالت بالا به حالت پایین تونل می زنند. بازپخت کوانتومی از برهم نهی همه حالات ممکن یک سیستم با وزن مساوی شروع می شود. سپس معادله شرودینگر وابسته به زمان، تکامل زمانی سیستم را هدایت می‌کند و با افزایش زمان، دامنه هر حالت را تحت تأثیر قرار می‌دهد. در نهایت، می توان به حالت پایه رسید تا همیلتونی آنی سیستم را به دست آورد.

مدار NISQ به عنوان مدل کوانتومی [ ویرایش ]

با پیشروی عمق مدار کوانتومی در دستگاه‌های NISQ ، سطح نویز افزایش می‌یابد و چالش قابل‌توجهی را برای محاسبه دقیق هزینه‌ها و گرادیان‌ها در مدل‌های آموزشی ایجاد می‌کند. تحمل نویز با استفاده از پرسپترون کوانتومی و الگوریتم کوانتومی در سخت‌افزار کوانتومی در دسترس بهبود می‌یابد. [ نیازمند منبع ]

اتصال منظم اجزای مشابهی که به عنوان نورون ها شناخته می شوند ، اساس حتی پیچیده ترین شبکه های مغزی را تشکیل می دهد. به طور معمول، یک نورون دو عملیات دارد: محصول داخلی و یک تابع فعال سازی . برخلاف تابع فعال‌سازی، که معمولاً غیرخطی است ، محصول داخلی یک فرآیند خطی است. با محاسبات کوانتومی، فرآیندهای خطی ممکن است به راحتی انجام شوند، به دلیل سادگی اجرا، تابع آستانه توسط اکثر نورون‌های کوانتومی برای توابع فعال‌سازی ترجیح داده می‌شود. [ نیازمند منبع ]

+ نوشته شده در جمعه بیستم بهمن ۱۴۰۲ ساعت 8:15 توسط علی رضا نقش |

کامپیوتر و ریاضی با علی رضا نقش

آموزش